Оптимизация системы сигналов

канд. биол. наук М.П.Иванов, д-р техн. наук В.В.Кашинов

ФНИИ им.А.А.Ухтомского, СПбГУ

Во многихсистемах, например, спутниковой навигационной системе GPS NAVSTAR, асинхронных адресныхсистемахсвязи (ААСС) и т.д. используются сигналы, излучаемые многими источниками на одной несущей частоте и адресованные разным потребителям. При этом для приема используется согласованная с тем сигналом, который нужно принять, фильтрация или корреляционный прием. Возможно, применение частотно-временной фильтрации [1]. В таких системах неизбежно появление перекрестных внутрисистемных помех, которые желательно минимизировать. В работе [2] показано, что при определении качества системы по среднему интегральному эффекту взаимных помех непрерывные сигналы должны иметь одинаковые автокорреляционные функции, то есть должны различаться только фазовыми характеристиками. Этот критерий целесообразно использовать, если взаимные корреляционные функции (ВКФ) имеют один значительный всплеск Rkm, которым,восновном,иопределяется критерий - величина, или, наоборот, имеют много всплесков одного порядка. Однако в упомянутой работе [2] не приведена процедура построения самой системы сигналов.

Примем за критерий оптимальности максимальную величину всплесков ВКФ, а сигналы оптимальной системы определим в классе функций, связанных между собой линейными операторами. Все реальные сигналы принадлежат энергетическому пространству L2, а общий вид линейного оператора, действующего из L2 в L2, - интегральный, поэтому искомая система сигналов является единственной.

Обозначим как искомую систему сигналов, построеннуюна базе некоторого основного (условного) сигнала S0 по правилу

 (1)

где Ak - линейный интегральный оператор с ядром hk (u):

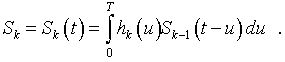 (2)

Будем считать основной сигнал S0 реализацией некоторого случайного стационарного процесса с интервалом корреляции tcor << T, получим для ВКФ Rkm k-го и m-го сигналов

 (3)

В частности, как известно [3],

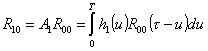 (4)

и

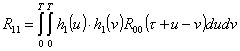 (5)

Экстремальные значения ВКФ всех сигналов Sk достигаются в моментывремени относительномаксимумаосновногосигналаx0, которые определяются уравнениями

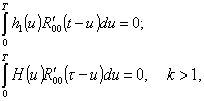 (6)

где H(u) - ядро произведения линейных интегральных операторов Ak Ak-1 -A1.

Чтобы исключить тривиальные решения Ak º 0, введем естественные ограничения на энергию функций hk(u):

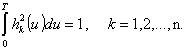 (7)

Тогда первая вариация функционала R10 с учетом ограничений (6) и (7) будет иметь вид

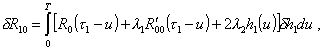 (8)

где l1 и l2 - неопределенные пока множители Лагранжа.

Используя результаты работы [4], получим обобщенное уравнение Эйлера-Пуассона для функции h1(u), доставляющей экстремум функционалу R10

 (9)

Множитель Лагранжа l2 находится при интегрировании по интервалу T обеих частей уравнения (9), умноженных на ядро h1(u), а множитель l1 - путем подобного интегрирования после возведения обеих частей уравнения в квадрат. Выполняя преобразования с учетом ограничений (6) и (7) и формулы (5), получим для ядра оператора A1, определяющего первый сигнал системы S1, и для корреляционной функции этого сигнала следующие выражения

Рекомендуем скачать другие рефераты по теме: образец курсовой работы, новейшие рефераты.





1  2  3  4 | Следующая страница реферата