
–Т–Њ—Б—Б—В–∞–љ–Њ–≤–ї–µ–љ–Є–µ —Н—В–∞–ї–Њ–љ–∞ —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤ –љ–∞ –Њ—Б–љ–Њ–≤–µ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П —Е–∞—Г—Б–і–Њ—А—Д–Њ–≤–Њ–є –Љ–µ—В—А–Є–Ї–Є –≤ —Д–∞–Ј–Њ–≤–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В
| –Ъ–∞—В–µ–≥–Њ—А–Є—П —А–µ—Д–µ—А–∞—В–∞: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –љ–∞—Г–Ї–µ –Є —В–µ—Е–љ–Є–Ї–µ
| –Ґ–µ–≥–Є —А–µ—Д–µ—А–∞—В–∞: –±–µ—Б–њ–ї–∞—В–љ—Л–µ —В–µ—Б—В—Л, —Б–Ї–∞—З–∞—В–Є —А–µ—Д–µ—А–∞—В
| –Ф–Њ–±–∞–≤–Є–ї(–∞) –љ–∞ —Б–∞–є—В: –Ф—А—С–Љ–Є–љ.
1 2 3 4 5 | –°–ї–µ–і—Г—О—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞
–Т–Њ—Б—Б—В–∞–љ–Њ–≤–ї–µ–љ–Є–µ —Н—В–∞–ї–Њ–љ–∞ —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤ –љ–∞ –Њ—Б–љ–Њ–≤–µ –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є—П —Е–∞—Г—Б–і–Њ—А—Д–Њ–≤–Њ–є –Љ–µ—В—А–Є–Ї–Є –≤ —Д–∞–Ј–Њ–≤–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В
–Ы–µ–Њ–љ–Є–і –°–Њ–ї–Њ–Љ–Њ–љ–Њ–≤–Є—З –§–∞–є–љ–Ј–Є–ї—М–±–µ—А–≥, –Ї.—В.–љ.
–Я—А–µ–і–ї–Њ–ґ–µ–љ–∞ —Б—В–Њ—Е–∞—Б—В–Є—З–µ—Б–Ї–∞—П –Љ–Њ–і–µ–ї—М –њ–Њ—А–Њ–ґ–і–µ–љ–Є—П —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤. –Я–Њ–Ї–∞–Ј–∞–љ–Њ, —З—В–Њ —Н—В–∞ –Љ–Њ–і–µ–ї—М —П–≤–ї—П–µ—В—Б—П –Њ–±–Њ–±—Й–µ–љ–Є–µ–Љ –Љ–Њ–і–µ–ї–µ–є –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Њ–є –Є –њ–Њ—З—В–Є –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Њ–є —Д—Г–љ–Ї—Ж–Є–є. –Я—А–µ–і–ї–Њ–ґ–µ–љ –Ї–Њ–љ—Б—В—А—Г–Ї—В–Є–≤–љ—Л–є –Љ–µ—В–Њ–і –Њ—Ж–µ–љ–Ї–Є —Н—В–∞–ї–Њ–љ–∞ –њ–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є–Є —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–Є–≥–љ–∞–ї–∞, –љ–∞–±–ї—О–і–∞–µ–Љ–Њ–≥–Њ –≤ —Д–∞–Ј–Њ–≤–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В.
–Т–≤–µ–і–µ–љ–Є–µ. –Я–Њ–≤—В–Њ—А—П—О—Й–Є–µ—Б—П –≤–Њ –≤—А–µ–Љ–µ–љ–Є –њ—А–Њ—Ж–µ—Б—Б—Л —З–∞—Б—В–Њ –њ—А–Њ—В–µ–Ї–∞—О—В –≤ —В–µ—Е–љ–Є—З–µ—Б–Ї–Є—Е –Є –±–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є—Е —Б–Є—Б—В–µ–Љ–∞—Е. –Ґ–∞–Ї–Є–µ –њ—А–Њ—Ж–µ—Б—Б—Л –њ–Њ—А–Њ–ґ–і–∞—О—В —Б–њ–µ—Ж–Є—Д–Є—З–µ—Б–Ї–Є–µ —Б–Є–≥–љ–∞–ї—Л, –Ї–Њ—В–Њ—А—Л–µ –≤ –љ–∞—Г—З–љ–Њ–є –ї–Є—В–µ—А–∞—В—Г—А–µ –њ—А–Є–љ—П—В–Њ –љ–∞–Ј—Л–≤–∞—В—М —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є–Љ–Є [1] –Є–ї–Є –Ї–≤–∞–Ј–Є–њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Є–Љ–Є [2]. –Ґ–Є–њ–Є—З–љ—Л–Љ–Є –њ—А–Є–Љ–µ—А–∞–Љ–Є —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤ —П–≤–ї—П—О—В—Б—П —Н–ї–µ–Ї—В—А–Њ–Ї–∞—А–і–Є–Њ–≥—А–∞–Љ–Љ–∞ (–≠–Ъ–У), —А–µ–Њ–≥—А–∞–Љ–Љ–∞, –Љ–∞–≥–љ–Є—В–Њ–Ї–∞—А–і–Є–Њ–≥—А–∞–Љ–Љ–∞ –Є –Љ–љ–Њ–≥–Є–µ –і—А—Г–≥–Є–µ —Д–Є–Ј–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є–µ —Б–Є–≥–љ–∞–ї—Л, –Њ—В—А–∞–ґ–∞—О—Й–Є–µ —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є–є —Е–∞—А–∞–Ї—В–µ—А —А–∞–±–Њ—В—Л —Б–Є—Б—В–µ–Љ—Л –Ї—А–Њ–≤–Њ–Њ–±—А–∞—Й–µ–љ–Є—П –ґ–Є–≤–Њ–≥–Њ –Њ—А–≥–∞–љ–Є–Ј–Љ–∞.
–Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ —Б—Г—Й–µ—Б—В–≤—Г—О—Й–Є–µ –Ї–Њ–Љ–њ—М—О—В–µ—А–љ—Л–µ —Б–Є—Б—В–µ–Љ—Л –∞–љ–∞–ї–Є–Ј–∞ –Є –Є–љ—В–µ—А–њ—А–µ—В–∞—Ж–Є–Є —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –≠–Ъ–У, –≤—Б–µ –µ—Й–µ –љ–µ –Њ–±–µ—Б–њ–µ—З–Є–≤–∞—О—В —В—А–µ–±—Г–µ–Љ—Г—О –і–Њ—Б—В–Њ–≤–µ—А–љ–Њ—Б—В—М —А–µ–Ј—Г–ї—М—В–∞—В–Њ–≤ [3]. –°–Њ–≥–ї–∞—Б–љ–Њ [4], —Н—В–Њ –≤ –њ–µ—А–≤—Г—О –Њ—З–µ—А–µ–і—М –≤—Л–Ј–≤–∞–љ–Њ –Њ—И–Є–±–Ї–∞–Љ–Є, –Ї–Њ—В–Њ—А—Л–µ –≤–Њ–Ј–љ–Є–Ї–∞—О—В –њ—А–Є –Є–Ј–Љ–µ—А–µ–љ–Є–Є –њ–∞—А–∞–Љ–µ—В—А–Њ–≤ (–і–Є–∞–≥–љ–Њ—Б—В–Є—З–µ—Б–Ї–Є—Е –њ—А–Є–Ј–љ–∞–Ї–Њ–≤) –њ—А–Є –Њ–±—А–∞–±–Њ—В–Ї–µ —А–µ–∞–ї—М–љ—Л—Е —Б–Є–≥–љ–∞–ї–Њ–≤ –≤–Њ –≤—А–µ–Љ–µ–љ–љ–Њ–є –Њ–±–ї–∞—Б—В–Є. –Ю–і–Є–љ –Є–Ј –∞–ї—М—В–µ—А–љ–∞—В–Є–≤–љ—Л—Е –Љ–µ—В–Њ–і–Њ–≤ –∞–љ–∞–ї–Є–Ј–∞ —В–∞–Ї–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤, –њ—А–µ–і–ї–Њ–ґ–µ–љ–љ—Л–є –≤ [5] –Є –њ–Њ–ї—Г—З–Є–≤—И–Є–є —А–∞–Ј–≤–Є—В–Є–µ –≤ —Ж–µ–ї–Њ–Љ —А—П–і–µ –і—А—Г–≥–Є—Е —А–∞–±–Њ—В, –≤ —З–∞—Б—В–љ–Њ—Б—В–Є, –≤
[6-8], –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В –Њ—В–Њ–±—А–∞–ґ–µ–љ–Є–µ –Є –Њ–±—А–∞–±–Њ—В–Ї—Г —Б–Є–≥–љ–∞–ї–∞ –≤ —Д–∞–Ј–Њ–≤–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ –Ї–Њ–Њ—А–і–Є–љ–∞—В.
–Т –љ–∞—Б—В–Њ—П—Й–µ–є —Б—В–∞—В—М–µ –њ—А–µ–і–ї–∞–≥–∞–µ—В—Б—П –Љ–Њ–і–µ–ї—М –њ–Њ—А–Њ–ґ–і–µ–љ–Є—П —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤ –Є –љ–∞ –Њ—Б–љ–Њ–≤–µ —Н—В–Њ–є –Љ–Њ–і–µ–ї–Є –Є—Б—Б–ї–µ–і—Г–µ—В—Б—П –љ–Њ–≤—Л–є –Љ–µ—В–Њ–і –≤–Њ—Б—Б—В–∞–љ–Њ–≤–ї–µ–љ–Є–µ —Н—В–∞–ї–Њ–љ–∞ —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Њ–≥–Њ —Б–Є–≥–љ–∞–ї–∞ –њ–Њ –Є—Б–Ї–∞–ґ–µ–љ–љ–Њ–є —А–µ–∞–ї–Є–Ј–∞—Ж–Є–Є, –љ–∞–±–ї—О–і–∞–µ–Љ–Њ–є –≤ —Д–∞–Ј–Њ–≤–Њ–Љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ.
–Я–Њ—Б—В–∞–љ–Њ–≤–Ї–∞
–Ј–∞–і–∞—З–Є. –Я—Г—Б—В—М –љ–∞–±–ї—О–і–∞–µ–Љ—Л–є —Б–Є–≥–љ–∞–ї ![]() —П–≤–ї—П–µ—В—Б—П
—А–µ–Ј—Г–ї—М—В–∞—В–Њ–Љ –Є—Б–Ї–∞–ґ–µ–љ–Є—П –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞
—П–≤–ї—П–µ—В—Б—П
—А–µ–Ј—Г–ї—М—В–∞—В–Њ–Љ –Є—Б–Ї–∞–ґ–µ–љ–Є—П –њ–µ—А–Є–Њ–і–Є—З–µ—Б–Ї–Њ–≥–Њ –њ—А–Њ—Ж–µ—Б—Б–∞ ![]() —Б–ї—Г—З–∞–є–љ—Л–Љ
–≤–Њ–Ј–Љ—Г—Й–µ–љ–Є–µ–Љ
—Б–ї—Г—З–∞–є–љ—Л–Љ
–≤–Њ–Ј–Љ—Г—Й–µ–љ–Є–µ–Љ ![]() , –≥–і–µ
, –≥–і–µ ![]() - –љ–µ–Ї–Њ—В–Њ—А–∞—П
—Д—Г–љ–Ї—Ж–Є—П. –Э–∞–Ј–Њ–≤–µ–Љ —Н—В–∞–ї–Њ–љ–љ—Л–Љ —Ж–Є–Ї–ї–Њ–Љ
- –љ–µ–Ї–Њ—В–Њ—А–∞—П
—Д—Г–љ–Ї—Ж–Є—П. –Э–∞–Ј–Њ–≤–µ–Љ —Н—В–∞–ї–Њ–љ–љ—Л–Љ —Ж–Є–Ї–ї–Њ–Љ ![]() - —З–∞—Б—В—М
–љ–µ–љ–∞–±–ї—О–і–∞–µ–Љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є
- —З–∞—Б—В—М
–љ–µ–љ–∞–±–ї—О–і–∞–µ–Љ–Њ–є —Д—Г–љ–Ї—Ж–Є–Є ![]() –љ–∞ –ї—О–±–Њ–Љ –Є–Ј –µ–µ
–њ–µ—А–Є–Њ–і–Њ–≤
–љ–∞ –ї—О–±–Њ–Љ –Є–Ј –µ–µ
–њ–µ—А–Є–Њ–і–Њ–≤ ![]() . –°—В–∞–≤–Є—В—Б—П
–Ј–∞–і–∞—З–∞ –Њ—Ж–µ–љ–Є—В—М —Н—В–∞–ї–Њ–љ
. –°—В–∞–≤–Є—В—Б—П
–Ј–∞–і–∞—З–∞ –Њ—Ж–µ–љ–Є—В—М —Н—В–∞–ї–Њ–љ ![]() –њ–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є–Є
–њ–Њ —А–µ–∞–ї–Є–Ј–∞—Ж–Є–Є ![]() , –љ–∞–±–ї—О–і–∞–µ–Љ–Њ–є
–љ–∞ –Њ—В—А–µ–Ј–Ї–µ
, –љ–∞–±–ї—О–і–∞–µ–Љ–Њ–є
–љ–∞ –Њ—В—А–µ–Ј–Ї–µ ![]() .
.
–°—В–Њ—Е–∞—Б—В–Є—З–µ—Б–Ї–∞—П
–Љ–Њ–і–µ–ї—М –њ–Њ—А–Њ–ґ–і–µ–љ–Є—П —Ж–Є–Ї–ї–Є—З–µ—Б–Ї–Є—Е —Б–Є–≥–љ–∞–ї–Њ–≤. –Я—А–µ–ґ–і–µ —З–µ–Љ –њ–µ—А–µ—Е–Њ–і–Є—В—М –Ї —А–µ—И–µ–љ–Є—О
–њ–Њ—Б—В–∞–≤–ї–µ–љ–љ–Њ–є –Ј–∞–і–∞—З–Є, —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ –Њ–і–љ—Г –Є–Ј –≤–Њ–Ј–Љ–Њ–ґ–љ—Л—Е –Љ–Њ–і–µ–ї–µ–є –њ–Њ—А–Њ–ґ–і–µ–љ–Є—П ![]() –њ–Њ —Н—В–∞–ї–Њ–љ—Г
–њ–Њ —Н—В–∞–ї–Њ–љ—Г![]() . –С—Г–і–µ–Љ
—Б—З–Є—В–∞—В—М, —З—В–Њ —Н—В–∞–ї–Њ–љ
. –С—Г–і–µ–Љ
—Б—З–Є—В–∞—В—М, —З—В–Њ —Н—В–∞–ї–Њ–љ ![]() –Љ–Њ–ґ–µ—В –±—Л—В—М
–њ—А–µ–і—Б—В–∞–≤–ї–µ–љ –≤ –≤–Є–і–µ —Д—Г–љ–Ї—Ж–Є–Є, –Ї—Г—Б–Њ—З–љ–Њ-–Ј–∞–і–∞–љ–љ–Њ–є –љ–∞ –Є–љ—В–µ—А–≤–∞–ї–µ
–Љ–Њ–ґ–µ—В –±—Л—В—М
–њ—А–µ–і—Б—В–∞–≤–ї–µ–љ –≤ –≤–Є–і–µ —Д—Г–љ–Ї—Ж–Є–Є, –Ї—Г—Б–Њ—З–љ–Њ-–Ј–∞–і–∞–љ–љ–Њ–є –љ–∞ –Є–љ—В–µ—А–≤–∞–ї–µ ![]() –Њ—В–і–µ–ї—М–љ—Л–Љ–Є
—Д—А–∞–≥–Љ–µ–љ—В–∞–Љ–Є
–Њ—В–і–µ–ї—М–љ—Л–Љ–Є
—Д—А–∞–≥–Љ–µ–љ—В–∞–Љ–Є
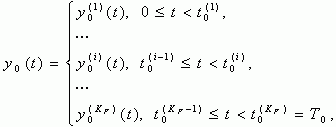 (1)
(1)
–њ–Њ–ї–∞–≥–∞—П, —З—В–Њ —З–Є—Б–ї–Њ —В–∞–Ї–Є—Е —Д—А–∞–≥–Љ–µ–љ—В–Њ–≤ ![]() .
–Я—А–Є–Љ–µ–љ–Є—В–µ–ї—М–љ–Њ –Ї –≠–Ъ–У —В–∞–Ї–Є–µ —Д—А–∞–≥–Љ–µ–љ—В—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В —Б—В–∞–і–Є—П–Љ –њ—А–Њ—Ж–µ—Б—Б–∞ –≤–Њ–Ј–±—Г–ґ–і–µ–љ–Є—П
–Њ—В–і–µ–ї—М–љ—Л—Е —Г—З–∞—Б—В–Ї–Њ–≤ —Б–µ—А–і—Ж–∞ - –і–µ–њ–Њ–ї—П—А–Є–Ј–∞—Ж–Є–Є –њ—А–µ–і—Б–µ—А–і–Є–є (–≤–Њ–ї–љ–µ
.
–Я—А–Є–Љ–µ–љ–Є—В–µ–ї—М–љ–Њ –Ї –≠–Ъ–У —В–∞–Ї–Є–µ —Д—А–∞–≥–Љ–µ–љ—В—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—В —Б—В–∞–і–Є—П–Љ –њ—А–Њ—Ж–µ—Б—Б–∞ –≤–Њ–Ј–±—Г–ґ–і–µ–љ–Є—П
–Њ—В–і–µ–ї—М–љ—Л—Е —Г—З–∞—Б—В–Ї–Њ–≤ —Б–µ—А–і—Ж–∞ - –і–µ–њ–Њ–ї—П—А–Є–Ј–∞—Ж–Є–Є –њ—А–µ–і—Б–µ—А–і–Є–є (–≤–Њ–ї–љ–µ![]() ), –≤–Њ–Ј–±—Г–ґ–і–µ–љ–Є—О
(–Ї–Њ–Љ–њ–ї–µ–Ї—Б—Г
), –≤–Њ–Ј–±—Г–ґ–і–µ–љ–Є—О
(–Ї–Њ–Љ–њ–ї–µ–Ї—Б—Г![]() ) –Є
—А–µ–њ–Њ–ї—П—А–Є–Ј–∞—Ж–Є–Є (–≤–Њ–ї–љ–µ
) –Є
—А–µ–њ–Њ–ї—П—А–Є–Ј–∞—Ж–Є–Є (–≤–Њ–ї–љ–µ ![]() ) –ґ–µ–ї—Г–і–Њ—З–Ї–Њ–≤
[1].
) –ґ–µ–ї—Г–і–Њ—З–Ї–Њ–≤
[1].
–Я—А–µ–і—Б—В–∞–≤–Є–Љ
–љ–∞–±–ї—О–і–∞–µ–Љ—Л–є —Б–Є–≥–љ–∞–ї ![]() –≤ –≤–Є–і–µ
–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є –Є—Б–Ї–∞–ґ–µ–љ–љ—Л—Е —Н—В–∞–ї–Њ–љ–Њ–≤ (1), –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—П, —З—В–Њ –љ–∞ –Ї–∞–ґ–і–Њ–Љ
–≤ –≤–Є–і–µ
–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є –Є—Б–Ї–∞–ґ–µ–љ–љ—Л—Е —Н—В–∞–ї–Њ–љ–Њ–≤ (1), –њ—А–µ–і–њ–Њ–ї–∞–≥–∞—П, —З—В–Њ –љ–∞ –Ї–∞–ґ–і–Њ–Љ ![]() -–Љ —Ж–Є–Ї–ї–µ —В–∞–Ї–Њ–є
–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є (
-–Љ —Ж–Є–Ї–ї–µ —В–∞–Ї–Њ–є
–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В–Є (![]() ) –Њ—В–і–µ–ї—М–љ—Л–µ
—Д—А–∞–≥–Љ–µ–љ—В—Л —Н—В–∞–ї–Њ–љ–∞
) –Њ—В–і–µ–ї—М–љ—Л–µ
—Д—А–∞–≥–Љ–µ–љ—В—Л —Н—В–∞–ї–Њ–љ–∞ ![]() –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ
–Њ–і–Є–љ –Њ—В –і—А—Г–≥–Њ–≥–Њ –ї–Є–љ–µ–є–љ–Њ —А–∞—Б—В—П–≥–Є–≤–∞—О—В—Б—П (—Б–ґ–Є–Љ–∞—О—В—Б—П) –њ–Њ –≤—А–µ–Љ–µ–љ–Є, –∞ —Б–∞–Љ–∞ —Д—Г–љ–Ї—Ж–Є—П
–љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ
–Њ–і–Є–љ –Њ—В –і—А—Г–≥–Њ–≥–Њ –ї–Є–љ–µ–є–љ–Њ —А–∞—Б—В—П–≥–Є–≤–∞—О—В—Б—П (—Б–ґ–Є–Љ–∞—О—В—Б—П) –њ–Њ –≤—А–µ–Љ–µ–љ–Є, –∞ —Б–∞–Љ–∞ —Д—Г–љ–Ї—Ж–Є—П ![]() –ї–Є–љ–µ–є–љ–Њ
—А–∞—Б—В—П–≥–Є–≤–∞–µ—В—Б—П (—Б–ґ–Є–Љ–∞–µ—В—Б—П) –њ–Њ –∞–Љ–њ–ї–Є—В—Г–і–µ. –Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ
–њ—А–Њ—Ж–µ—Б—Б –њ–Њ—А–Њ–ґ–і–µ–љ–Є—П
–ї–Є–љ–µ–є–љ–Њ
—А–∞—Б—В—П–≥–Є–≤–∞–µ—В—Б—П (—Б–ґ–Є–Љ–∞–µ—В—Б—П) –њ–Њ –∞–Љ–њ–ї–Є—В—Г–і–µ. –Ш–љ—Л–Љ–Є —Б–ї–Њ–≤–∞–Љ–Є, –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ
–њ—А–Њ—Ж–µ—Б—Б –њ–Њ—А–Њ–ґ–і–µ–љ–Є—П ![]() -–≥–Њ —Д—А–∞–≥–Љ–µ–љ—В–∞
(
-–≥–Њ —Д—А–∞–≥–Љ–µ–љ—В–∞
(![]() ) –Ї–∞–ґ–і–Њ–≥–Њ
) –Ї–∞–ґ–і–Њ–≥–Њ ![]() -–≥–Њ —Ж–Є–Ї–ї–∞ (
-–≥–Њ —Ж–Є–Ї–ї–∞ (![]() )
–Њ—Б—Г—Й–µ—Б—В–≤–ї—П–µ—В—Б—П –љ–∞ –Њ—Б–љ–Њ–≤–µ –Њ–њ–µ—А–∞—В–Њ—А–љ–Њ–≥–Њ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П
)
–Њ—Б—Г—Й–µ—Б—В–≤–ї—П–µ—В—Б—П –љ–∞ –Њ—Б–љ–Њ–≤–µ –Њ–њ–µ—А–∞—В–Њ—А–љ–Њ–≥–Њ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П
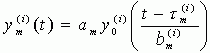 , (2)
, (2)
–≥–і–µ
![]() -
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –њ–∞—А–∞–Љ–µ—В—А—Л –ї–Є–љ–µ–є–љ–Њ–≥–Њ —А–∞—Б—В—П–ґ–µ–љ–Є—П (—Б–ґ–∞—В–Є—П) –њ–Њ –∞–Љ–њ–ї–Є—В—Г–і–µ –Є –≤—А–µ–Љ–µ–љ–Є, –∞
-
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ –њ–∞—А–∞–Љ–µ—В—А—Л –ї–Є–љ–µ–є–љ–Њ–≥–Њ —А–∞—Б—В—П–ґ–µ–љ–Є—П (—Б–ґ–∞—В–Є—П) –њ–Њ –∞–Љ–њ–ї–Є—В—Г–і–µ –Є –≤—А–µ–Љ–µ–љ–Є, –∞ ![]() - —Б–і–≤–Є–≥ –њ–Њ
–≤—А–µ–Љ–µ–љ–Є. –Ф–ї—П –Њ–±–µ—Б–њ–µ—З–µ–љ–Є—П –љ–µ–њ—А–µ—А—Л–≤–љ–Њ—Б—В–Є –њ–Њ—А–Њ–ґ–і–∞–µ–Љ–Њ–≥–Њ —Б–Є–≥–љ–∞–ї–∞ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ
- —Б–і–≤–Є–≥ –њ–Њ
–≤—А–µ–Љ–µ–љ–Є. –Ф–ї—П –Њ–±–µ—Б–њ–µ—З–µ–љ–Є—П –љ–µ–њ—А–µ—А—Л–≤–љ–Њ—Б—В–Є –њ–Њ—А–Њ–ґ–і–∞–µ–Љ–Њ–≥–Њ —Б–Є–≥–љ–∞–ї–∞ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞–µ—В—Б—П, —З—В–Њ
![]() –Я–Њ—Б–ї–µ–і–љ–µ–µ
—В—А–µ–±–Њ–≤–∞–љ–Є–µ –≤—Б–µ–≥–і–∞ –Љ–Њ–ґ–љ–Њ –Њ–±–µ—Б–њ–µ—З–Є—В—М, –≤—Л–њ–Њ–ї–љ–Є–≤ –њ—А–µ–і–≤–∞—А–Є—В–µ–ї—М–љ—Г—О –љ–Њ—А–Љ–Є—А–Њ–≤–Ї—Г —Н—В–∞–ї–Њ–љ–∞
–Я–Њ—Б–ї–µ–і–љ–µ–µ
—В—А–µ–±–Њ–≤–∞–љ–Є–µ –≤—Б–µ–≥–і–∞ –Љ–Њ–ґ–љ–Њ –Њ–±–µ—Б–њ–µ—З–Є—В—М, –≤—Л–њ–Њ–ї–љ–Є–≤ –њ—А–µ–і–≤–∞—А–Є—В–µ–ї—М–љ—Г—О –љ–Њ—А–Љ–Є—А–Њ–≤–Ї—Г —Н—В–∞–ї–Њ–љ–∞
![]() .
.
–Я—Г—Б—В—М
–≤ –њ—А–µ–і–µ–ї–∞—Е –Ї–∞–ґ–і–Њ–≥–Њ ![]() -–≥–Њ —Ж–Є–Ї–ї–∞
–њ–∞—А–∞–Љ–µ—В—А
-–≥–Њ —Ж–Є–Ї–ї–∞
–њ–∞—А–∞–Љ–µ—В—А ![]() –њ—А–Є–љ–Є–Љ–∞–µ—В
—Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ
–њ—А–Є–љ–Є–Љ–∞–µ—В
—Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ
![]() , (3)
, (3)
–≥–і–µ
![]() -
–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М —А–µ–∞–ї–Є–Ј–∞—Ж–Є–є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е —Б–ї—Г—З–∞–є–љ—Л—Е –≤–µ–ї–Є—З–Є–љ, –Ї–Њ—В–Њ—А—Л–µ —Б –љ—Г–ї–µ–≤—Л–Љ
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–ґ–Є–і–∞–љ–Є–µ–Љ
-
–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М —А–µ–∞–ї–Є–Ј–∞—Ж–Є–є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е —Б–ї—Г—З–∞–є–љ—Л—Е –≤–µ–ї–Є—З–Є–љ, –Ї–Њ—В–Њ—А—Л–µ —Б –љ—Г–ї–µ–≤—Л–Љ
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–ґ–Є–і–∞–љ–Є–µ–Љ ![]() —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л
–љ–∞ –Є–љ—В–µ—А–≤–∞–ї–µ
—А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л
–љ–∞ –Є–љ—В–µ—А–≤–∞–ї–µ ![]() , –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–Љ
—Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–Љ —З–Є—Б–ї–Њ–Љ
, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–Њ–Љ
—Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–Љ —З–Є—Б–ї–Њ–Љ ![]() .
.
–Я—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ
—В–∞–Ї–ґ–µ, —З—В–Њ –њ–∞—А–∞–Љ–µ—В—А ![]() –њ—А–Є–љ–Є–Љ–∞–µ—В
—Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –≤ –њ—А–Њ—Ж–µ—Б—Б–µ –њ–Њ—А–Њ–ґ–і–µ–љ–Є—П –Ї–∞–ґ–і–Њ–≥–Њ
–њ—А–Є–љ–Є–Љ–∞–µ—В
—Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ–Њ–µ –Ј–љ–∞—З–µ–љ–Є–µ –≤ –њ—А–Њ—Ж–µ—Б—Б–µ –њ–Њ—А–Њ–ґ–і–µ–љ–Є—П –Ї–∞–ґ–і–Њ–≥–Њ ![]() -–≥–Њ —Д—А–∞–≥–Љ–µ–љ—В–∞
-–≥–Њ —Д—А–∞–≥–Љ–µ–љ—В–∞ ![]() -–≥–Њ —Ж–Є–Ї–ї–∞
-–≥–Њ —Ж–Є–Ї–ї–∞
![]() , (4)
, (4)
–≥–і–µ
![]() -
–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М —А–µ–∞–ї–Є–Ј–∞—Ж–Є–є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е —Б–ї—Г—З–∞–є–љ—Л—Е –≤–µ–ї–Є—З–Є–љ, –Ї–Њ—В–Њ—А—Л–µ —Б –љ—Г–ї–µ–≤—Л–Љ
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–ґ–Є–і–∞–љ–Є–µ–Љ
-
–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ—Б—В—М —А–µ–∞–ї–Є–Ј–∞—Ж–Є–є –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е —Б–ї—Г—З–∞–є–љ—Л—Е –≤–µ–ї–Є—З–Є–љ, –Ї–Њ—В–Њ—А—Л–µ —Б –љ—Г–ї–µ–≤—Л–Љ
–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є–Љ –Њ–ґ–Є–і–∞–љ–Є–µ–Љ ![]() —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л
–љ–∞ –Є–љ—В–µ—А–≤–∞–ї–∞—Е
—А–∞—Б–њ—А–µ–і–µ–ї–µ–љ—Л
–љ–∞ –Є–љ—В–µ—А–≤–∞–ї–∞—Е ![]() , –Њ–≥—А–∞–љ–Є—З–µ–љ–љ—Л–Љ–Є —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є
, –Њ–≥—А–∞–љ–Є—З–µ–љ–љ—Л–Љ–Є —Д–Є–Ї—Б–Є—А–Њ–≤–∞–љ–љ—Л–Љ–Є —З–Є—Б–ї–∞–Љ–Є ![]() .
.
–Я—А–Є
—В–∞–Ї–Є—Е –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є—П—Е –њ—А–Њ–і–Њ–ї–ґ–Є—В–µ–ї—М–љ–Њ—Б—В—М ![]() -–≥–Њ —Д—А–∞–≥–Љ–µ–љ—В–∞
-–≥–Њ —Д—А–∞–≥–Љ–µ–љ—В–∞ ![]() -–≥–Њ —Ж–Є–Ї–ї–∞
—Б–Є–≥–љ–∞–ї–∞
-–≥–Њ —Ж–Є–Ї–ї–∞
—Б–Є–≥–љ–∞–ї–∞ ![]() —Б–≤—П–Ј–∞–љ–∞ —Б
–њ—А–Њ–і–Њ–ї–ґ–Є—В–µ–ї—М–љ–Њ—Б—В—М—О
—Б–≤—П–Ј–∞–љ–∞ —Б
–њ—А–Њ–і–Њ–ї–ґ–Є—В–µ–ї—М–љ–Њ—Б—В—М—О ![]() —Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–≥–Њ
—Д—А–∞–≥–Љ–µ–љ—В–∞ —Н—В–∞–ї–Њ–љ–∞ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г—О—Й–µ–≥–Њ
—Д—А–∞–≥–Љ–µ–љ—В–∞ —Н—В–∞–ї–Њ–љ–∞ —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–µ–Љ
![]() .
.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, –Њ–±—Й–∞—П –њ—А–Њ–і–Њ–ї–ґ–Є—В–µ–ї—М–љ–Њ—Б—В—М ![]() -–≥–Њ —Ж–Є–Ї–ї–∞
–њ–Њ—А–Њ–ґ–і–∞–µ–Љ–Њ–≥–Њ —Б–Є–≥–љ–∞–ї–∞
-–≥–Њ —Ж–Є–Ї–ї–∞
–њ–Њ—А–Њ–ґ–і–∞–µ–Љ–Њ–≥–Њ —Б–Є–≥–љ–∞–ї–∞ ![]() –Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П
–≤—Л—А–∞–ґ–µ–љ–Є–µ–Љ
–Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П
–≤—Л—А–∞–ґ–µ–љ–Є–µ–Љ
![]() ,
,
–љ–∞—З–∞–ї—Г
![]() -–≥–Њ —Ж–Є–Ї–ї–∞
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Љ–Њ–Љ–µ–љ—В –≤—А–µ–Љ–µ–љ–Є
-–≥–Њ —Ж–Є–Ї–ї–∞
—Б–Њ–Њ—В–≤–µ—В—Б—В–≤—Г–µ—В –Љ–Њ–Љ–µ–љ—В –≤—А–µ–Љ–µ–љ–Є
![]() ,
,
–†–µ–Ї–Њ–Љ–µ–љ–і—Г–µ–Љ —Б–Ї–∞—З–∞—В—М –і—А—Г–≥–Є–µ —А–µ—Д–µ—А–∞—В—Л –њ–Њ —В–µ–Љ–µ: –Њ—В—З–µ—В –њ–Њ –њ—А–∞–Ї—В–Є–Ї–µ, —А–µ—И–µ–±–љ–Є–Ї 11 –Ї–ї–∞—Б—Б.
–Ъ–∞—В–µ–≥–Њ—А–Є–Є:
1 2 3 4 5 | –°–ї–µ–і—Г—О—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞
 –У–ї–∞–≤–љ–∞—П
–У–ї–∞–≤–љ–∞—П