
К методике преподавания прикладной математики в военно-инженерном вузе
| Категория реферата: психология, педагогика
| Теги реферата: украинские рефераты, конспекты старшая группа
| Добавил(а) на сайт: Якушкин.
Предыдущая страница реферата | 1 2 3 4 | Следующая страница реферата
 Рис.2
Рис.2
Вернемся теперь к изображенному на рис. 1 процессу обслуживания и выпишем вероятности P1 и P2 - вероятности перехода узла в состояния s1 и s2 соответственно. (Существенно, что P1 и P2 не зависят от исходного состояния узла). Из условий задачи
|
|
(1) |
Теперь процесс обслуживания можно изобразить в виде последовательности "произвольных" событий (s1 и s2):
с
вероятностью P1 в состояние s1 через время t1 ![]() с вероятностью P2=1-P1 в состояние s2 через
время t2
с вероятностью P2=1-P1 в состояние s2 через
время t2
Рис.3
Введем далее следующие обозначения: N - количество последовательных событий обслуживания узла (замен); T(N) - длина соответствующего временного интервала; S(N) - суммарная стоимость N событий.
Используя рис.3 и определение вероятности события, легко показать, что
|
|
= |
NP1s1+NP2s2, |
(2) |
|
|
= |
|
(3) |
где
![]() -
математическое ожидание случайной величины
-
математическое ожидание случайной величины ![]() .
.
Из (2) и (3) получаем предварительный вид I - искомой средней интенсивности затрат на обслуживание узла:
|
|
(4) |
Теперь
необходимо получить явный вид ![]() . В смысле
физического понимания процесса обслуживания и необходимой математической
техники это наиболее сложная для курсанта промежуточная задача. Однако и для ее
решения не требуется знаний, выходящих за пределы стандартного курса
математики.
. В смысле
физического понимания процесса обслуживания и необходимой математической
техники это наиболее сложная для курсанта промежуточная задача. Однако и для ее
решения не требуется знаний, выходящих за пределы стандартного курса
математики.
Выделим
из реального процесса (см. рис.1) последовательность интервалов ![]() , т.е.
интервалов, завершающихся отказом. Обозначим затем через
, т.е.
интервалов, завершающихся отказом. Обозначим затем через ![]() плотность
вероятности продолжительности безотказной работы узла при условии его отказа в
интервале
плотность
вероятности продолжительности безотказной работы узла при условии его отказа в
интервале ![]() . Из
определения математического ожидания
. Из
определения математического ожидания
|
|
(5) Рекомендуем скачать другие рефераты по теме: реферат по обж, отчет о прохождении практики. Категории:Предыдущая страница реферата | 1 2 3 4 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
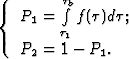
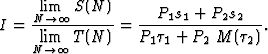
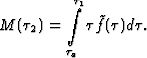
 Главная
Главная