Выпишем
условия, задающие 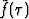 :
:
|
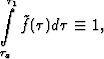
|
(6)
|
|
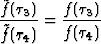
|
(7)
|
-
для любых 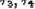 из
из 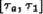 .
.
Условие
(6) очевидно. Условие (7) может потребовать отдельного разъяснения: оно
определяется тем, что поведение узла не зависит от того, какое подмножество
реального процесса мы рассматриваем (рис.4).
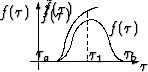 Рис.4
Рис.4
Определяя
из (6) и (7) явный вид 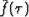 , подставляя
его в (5) и преобразуя, получаем
, подставляя
его в (5) и преобразуя, получаем
|
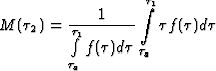
|
(8)
|
Мы
получили явный вид 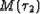 - средней
продолжительности безотказной работы узла при условии его отказа в интервале
- средней
продолжительности безотказной работы узла при условии его отказа в интервале 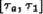 . Подставляя
(8) в (4) и преобразуя, получаем окончательно
. Подставляя
(8) в (4) и преобразуя, получаем окончательно
|
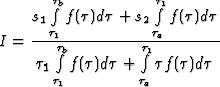
|
(9)
|
Очевидно, что задачу 1 можно дополнить требованием указать возможные способы определения
оптимального 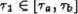 , обеспечивающего при данных s1,s2 и
, обеспечивающего при данных s1,s2 и 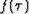 минимум I .
(например, из условия
минимум I .
(например, из условия 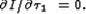 ) Требование
получить соответствующую расчетную формулу представляется здесь чрезмерным.
Однако находится достаточно эффектный и, как нам представляется, методически
результативный ход, позволяющий курсанту без больших технических затруднений
"поверить" в полученный результат. Для этого можно ослабить одно из
ограничений задачи 1:
) Требование
получить соответствующую расчетную формулу представляется здесь чрезмерным.
Однако находится достаточно эффектный и, как нам представляется, методически
результативный ход, позволяющий курсанту без больших технических затруднений
"поверить" в полученный результат. Для этого можно ослабить одно из
ограничений задачи 1:
Задача
2.
Найти
оптимальное значение 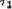 , обеспечивающее
минимум средней интенсивности затрат I для случая s1=s2=s0.
, обеспечивающее
минимум средней интенсивности затрат I для случая s1=s2=s0.
Решения
задачи 2
Поскольку
s0 - параметр задачи, а сумма интегралов числителя в (9) - тождественная
единица, задача сводится к исследованию на минимум функции
|
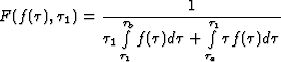
|
(10)
|
Достаточно, таким образом, решить относительно 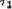 уравнение
уравнение
|
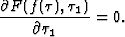
|
(11)
|
Поскольку
(см. рис.2) знаменатель в (10) всегда положителен, для решения (11) достаточно
знания основных правил дифференцирования и умения дифференцировать определенный
интеграл по одному из его пределов. В результате (11) легко сводится к
уравнению
Рекомендуем скачать другие рефераты по теме: реферат по обж, отчет о прохождении практики.
Предыдущая страница реферата |
1
2
3
4 |
Следующая страница реферата

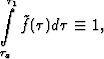
 Рис.4
Рис.4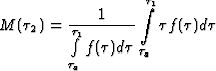
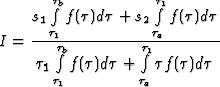
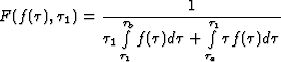
 Главная
Главная