Степень и логарифм
числа. Показательная и логарифмическая функции.
— любые действительные числа, то 1) а° = 1; 2) 3) 4) 5) 6) Логарифмом положительного числа b по основанию а (а > 0; а # 1) называется показатель степени, вкоторую нужно возвести основание а, чтобы получить b. Обозначение: logab (Iog10 b = lg b, logeb = In b). Определение логарифма записывается в виде равенства alogab = b которое называется основным логарифмическим тождеством. Из этого тождества и свойств степени вытекают следующие свойства логарифмов: 1) 2) 3) 4) Эти равенства справедливы для любых чисел b, b1, b2> 0; а, с > 0 и не равных единице, любого Отдельно отметим, что loga х2 = 2loga| x|. Наконец, из определения логарифма вытекает формула решения простейшего логарифмического уравнения:
Простейшее показательное уравнение решается, также исходя из определения логарифма и свойств степени, следующим образом: аx = b => х = loga b при b > 0 и а # 1,а >0. Если же
то, очевидно,
Также отдельно в показательном уравнении следует рассматривать случай a = 1. Очевидно, что уравнение 1x = b справедливо при всех х € R, если b = 1, а если b # 1, то
Более сложные уравнения сводятся к рассмотренным простейшим с помощью тождественных преобразований обеих частей уравнений. Используя основные свойства степени и логарифма, решите показательные и логарифмические уравнения (1-40): Задание 1.
Ответ: -6 Задание 2.
Ответ: 3 Задание 3.
Ответ: -4 Задание 4.
Ответ:
Задание 5.
Ответ:
Задание 6.
Решение: Так как 16 = 24, 0,5 = 2-1 и 8 = 23, то уравнение можно представить в виде
корнями которого и являются числа - 10 и 0. Ответ: {-10; 0} Задание 7.
Ответ: 81 Задание 8.
Ответ: {0; 25) Задание 9.
Решение: Так как
то из исходного уравнения получаем 1 + | х | = 2, или |х| = 1, откуда х = ± 1. Ответ: (-1; 1} Задание 10.
Ответ:
Задание 11.
Ответ:
Задание 12. 2 -|3x - 5| = 4 • 8 | x - 1| Ответ:
Задание 13. 3х-1 = 182x • Зх+1 • 2-2x Решение: Так как 182x = 344x • 22x, то из исходного уравнения получается уравнение 3x-1 = 35x+1, откуда
Ответ:
Задание 14. 2x • 3x-1 = 6x • 3x+1 Ответ: -2 Задание 15. 2x • 5x-1 = 0,2 • 102-x Ответ: 1 Задание 16. 4x • 5x+1 = 100 • 201-x Ответ: 1 Задание 17.
Ответ: {-2,5; 3} Задание 18.
Ответ: 4 Задание 19.
Ответ: 9 Задание 20.
Ответ:
Задание 21.
Ответ: {-3; 1} Задание 22. 2x + 2x-1 + 2x-2 = 3x - 3x-1 + 3x-2 Решение: Уравнение легко преобразуется к виду
Ответ: 2 Задание 23.
Ответ: 1,5 Задание 24.
Ответ:
Задание 25.
Ответ: 3 Задание 26. З12x-1 - 966x-1 - 274x-1 + 813x-1 = 2192 Ответ: 0,25 Задание 27. Iog3 (2x - 1) = 3 Ответ: 14 Задание 28.
Ответ: 11 Задание 29.
Ответ: {-1; 4} Задание 30.
Решение: Учитывая, что
получаем
или х2 - bх + 4 = 0, откуда х = 1 и х = 4. Ответ: {1; 4} Задание 31.
Ответ: 3 Задание 32.
Ответ: 3 Задание 33. Iog3 (1 + Iog3(2x -7)) = 1 Ответ: 4 Задание 34.
Ответ: 3 Задание 35. Iog2-x4 = 2 Решение: Исходное уравнение преобразуется к виду (2 - х)2 = 4, где 2 - x > 0 и 2 - x # 1. С учетом этих условий х = 0. Ответ: 0 Задание 36. logx+1 (x2 + 8x + 37) = 2 Решение: Исходное уравнение преобразуется к виду (х + 1)2 = х2 + 8х + 37, решением этого уравнения является значение х = -6, но оно не удовлетворяет условию х + 1 > 0. Ответ:
Задание 37. logx (2x2 - 7x + 12) = 2 Ответ: 3; 4 Задание 38.
Ответ: -1 Задание 39. Iog2 (2 • 4x-2 - 1) = 2x - 4 Ответ: 2 Задание 40. Iog2 (9 - 2x) = 100lg(x-3) Решение: Так как 10lg(x-3) = х - 3, где х - 3 > 0, то из исходного уравнения получаем уравнение 9 - 2x = 2x-3, откуда 2x = 8 или х = 3, но это значение не удовлетворяет условию х — 3 > 0. Ответ:
Задание 41. x Iog2 x2 + 1 = 2х + Iog2 x Решение: Исходное уравнение преобразуется к виду 2x(log2 х - 1) - (Iog2 х - 1) = 0, или (2х - 1)(log2 х - 1) = 0, откуда х = 0,5 и х = 2. Ответ: {0,5; 2} Задание 42. Iog2 x Iog3 x = Iog2 x2 + Iog3 x3 - 6 Ответ: 8; 9 Задание 43. Iog3 x Iog4 x = Iog3 x3 + Iog4 x4 - 12 Ответ: {64; 81} Задание 44.
Ответ:
Задание 45.
Ответ:
Решите уравнения 46—51, предварительно приведя входящие в них логарифмы к одному основанию: Задание 46. Iog16x + Iog4 x + Iog2 x = 7 Решение: Переходя во всех логарифмах к основанию 2, получим уравнение
откуда х = 16. Ответ: 16 Задание 47.
Ответ: 4 Задание 48.
Ответ:
Задание 49. Iog2 x + Iog3 x = 1 Ответ:
Задание 50.
Ответ:
Задание 51.
Ответ:
Задание 52.
Решение: При выполнении условий
исходное уравнение переходит в уравнение
корнями которого являются числа
Первое из этих значений удовлетворяет приведенным выше неравенствам, а второе — нет. Ответ:
Задание 53.
Ответ:
Задание 54.
Ответ:
Задание 55.
Ответ: 6 Задание 56. Iog2(3x + 5) = 3 - Iog2(x + 1) Ответ:
Задание 57. Iog4(x + 3) - Iog4(x - 1) = 2 - Iog4 8 Ответ: 5 Задание 58.
Ответ: -3 Задание 59. Iog9(x + 1) - log9(1 - x) = log9(2x + 3) Ответ:
Задание 60.
Ответ: 15 Задание 61.
Ответ:
Задание 62. 2 log3(x - 2) + Iog3(x - 4)2 = 0 Ответ:
Задание 63. lg(3x - 4)2 + lg(2x - 4)2 = 2 Ответ:
Задание 64. Ответ: 29 Задание 65.
Ответ: 13 Задание 66.
Решение: При выполнении условий tg 2x > 0 и ctg х < 0 исходное уравнение преобразуется в уравнение
которое распадается на совокупность уравнений tg х = 0 и tg2 х = 3, откуда
Выше приведенные неравенства выполняются только при
где n € Z. Ответ:
Задание 67.
Ответ:
Задание 68. Ig sin x = Ig cos x + Ig 2 Ответ: arctg 2 + 2 Пn; n € Z Задание 69. Iog2 sin x + Iog2 cos x + Iog2 tg x = -1 Ответ:
Задание 70.
Ответ:
Задание 71.
Ответ:
Задание 72. Iog2(15 sin2 x + 7sin x) = 1 + Iog2(3 sin x+ 1) Ответ:
Задание 73. 1 + Iog3(5 cos2 x - 3 cos x - 1) = Iog3(1 - 2 cos x) Ответ:
Задание 74. Iog2(4 cos x + 3) Iog6(4 cos x + 3) = Iog2(4 cos x + 3) + Iog6(4 cos x + 3) Решение: Перейдем к логарифмам по основанию 2, воспользовавшись тождеством
С помощью подстановки Iog2 (4 cos х + 3) = t исходное уравнение преобразуется в уравнение
которое распадается на совокупность уравнений t = 0 и t = 1 + Iog2 6, откуда 4 cos x + 3 = 1 и 4 cos x + 3 = 12. Второе уравнение не имеет решений, а из первого находим
Ответ:
Задание 75. Iog3(6 sin x + 4) Iog5(6 sin x + 4) = Iog3(6 sin x + 4) + Iog5(6 sin x + 4) Ответ:
Задание 76.
Решение: Преобразуя правую часть уравнения к виду
получим уравнение
при условии, что
Тригонометрическое уравнение преобразуется в уравнение
откуда
Наконец, учитывая, что х € (-2; 0) U (0; 2), получаем ответ. Ответ:
Задание 77.
Ответ:
Задание 78.
Ответ:
Задание 79.
Ответ:
Задание 80.
Ответ:
Решите уравнения 81—108, сводя их к квадратным после преобразований и подходящей замены переменной: Задание 81. 4x - 10 • 2x-1 =24 Решение: Вводя замену 2x = t > 0, получаем уравнение t2 - 5t - 24 = 0, откуда t = -3 и t = 8. Первое значение не удовлетворяет неравенству t > 0, а второе дает уравнение 2x = 8, т. е. х = 3. Ответ: 3 Задание 82. 92x+4 + 4 =26 • 32x+3 + 3 Ответ: -1 Задание 83.
Ответ: 1 Задание 84.
Ответ: -2 Задание 85. 3 • 22-x -2x-1 - 5 = 0 Ответ: 1 Задание 86. 3x+3 - З-x-1 -8 = 0 Ответ: -1 Задание 87.
Ответ: 1 Задание 88.
Ответ: -1; 1 Задание 89.
Ответ: 0 Задание 90. log22 x + Iog2 х - 6 = 0 Ответ:
Задание 91. log23 x - Iog3 х - 12 = 0 Ответ:
Задание 92. lg (х2 + 1) - 2 lg-1 (х2 +1) -1 Ответ: {-3; 3} Задание 93.
Ответ:
Задание 94.
Ответ:
Задание 95.
Ответ: {10; 100} Задание 96.
Ответ:
Задание 97.
Ответ:
Задание 98. 2 logx+2 5 + 1 = Iog5 (x + 2) Ответ:
Задание 99.
Ответ:
Задание 100.
Решение: Так как
то вводя обозначение
откуда
или
Ответ: {-3; 3} Задание 101.
Решение: Полагая
получим уравнение
откуда
Так как
то из уравнений
находим x = +4. Ответ: {-4; 4} Задание 102. log32 (4x - 3) + Iog3 (4x - 3) - 2 = 0 Ответ:
Задание 103.
Решение: Используя замену
получим уравнение
Отсюда
причем
не удовлетворяет неравенству 2t - 1 > 0. Из уравнения
находим
Ответ:
Задание 104. lg (lg x) + lg (lg (x3) - 2) = 0 Решение: Используя замену lg х = t, получим уравнение lg t + lg(3t - 2) = 0 или уравнение
Отсюда t = Igx = 1
и x = 10. Ответ: 10 Задание 105. 8 • 9x + 6x+11 = 27 • 4x Решение: Разделим обе части уравнения на 4x и введем обозначение
Полученное уравнение 8t2 + б? - 27 = 0 имеет корни
последний из которых не удовлетворяет неравенству t > 0. Из уравнения
находим х = 1. Ответ: 1 Задание 106.
Ответ: {1; Iog3/2 12} Задание 107.
Ответ: 4 Задание 108.
Ответ:
Задание 109.
Решение: Так как
то решениями
Замечание: При решении задач такого рода нет необходимости решать все входящие в их состав уравнения. Достаточно решить одно из них и отобрать те корни, которые удовлетворяют и другим уравнениям. Ответ: 0 Задание 110.
Ответ: -1 Задание 111.
Решение: Функция у = 3x-2 строго монотонно возрастает и положительна, а функция
там где она положительна, т. е. при х > 0, строго монотонно убывает, поэтому графики функций имеют единственную точку пересечения при х = 3. Ответ: 3 Задание 112.
Ответ: 1 Задание 113. 27 • 4x +7 • 9x =15 • 25x Решение: Корень
легко угадать, но нужно доказать, что это решение единственное. Разделим обе части уравнения на 9x и получим уравнение
Так как
то функция
строго монотонно убывает, а функция
где
строго монотонно возрастает. Отсюда и вытекает единственность решения. Ответ:
Задание 114.
Ответ:
Задание 115.
Ответ:
Задание 116.
Решение: Прологарифмируем обе части уравнения по любому основанию, например, по основанию 2. Получим уравнение (х2 - х - 1)log2 (x + 5) = (2х + 3) log2 (x + 5), которое распадается на совокупность уравнений log2 (x + 5) = 0 и х2 - х - 1 = 2х + 3. Первое из них имеет корень х = -4, а второе — корни х = -1 и х = 4, причем оба эти значения удовлетворяют неравенству х + 5 > 0. Ответ: {-4; -1; 4) Задание 117.
Ответ: {-1; 1; 2} Задание 118. х3lgx = 10х2 Ответ:
Задание 119.
Ответ:
Задание 120.
Ответ:
Задание 121.
Ответ:
Задание 122. 22x+1 - 5 • 6x + 3 • 9x = 0 Ответ: {-1; 0) Задание 123.
Ответ: 0 Задание 124.
Ответ: 9 Задание 125.
Ответ: {-1; 9) Задание 126.
Ответ:
Задание 127.
Ответ:
Задание 128. 3lg tg x - 2 • 3lg ctg x+1 = 1 Ответ: arctg 10 + Пn; n € Z Задание 129.
Ответ:
Задание 130. logx 2 • log2x2 = log4x2 Ответ:
Задание 131.
Ответ:
Задание 132.
Ответ:
Задание 133.
Ответ:
Задание 134.
Ответ: {3; 81} Задание 135.
Ответ: 4 Задание 136.
Ответ: 2 Задание 137.
Ответ: log3 2 Задание 138.
Ответ: 0 Задание 139.
Ответ:
Задание 140. 8x + 18x = 2 • 27x Ответ: 0 Задание 141. 5 • 32x + 15 • 52x-1 = 8 • 15x Ответ: {0; 1} Задание 142. 2(x)lg x + 3x-lg x = 5 Ответ:
Задание 143.
Ответ: 4 Задание 144.
Ответ:
Задание 145. 1 + logx-2(4x - 11) = 2 log4x-11 (4x2 - 19x + 22) Ответ: 5 Задание 146. Iog3x+7(9 + 12x + 4x2) + Iog2x+3 (6x2 + 23x + 21) = 4 Ответ:
Задание 147.
Ответ: {1; 3} Задание 148. 9 logsin 2x (4 cos2 x) + 8 Iog2cos x (sin x) = 16 Ответ:
Задание 149. (tg x)2 sin x = 1 Ответ:
Задание 150. (1 - cos x)sin x = 1 Ответ:
Задание 151.
Ответ:
Задание 152.
Ответ:
Задание 153.
Ответ:
Задание 154.
Решение: Наименьшее значение выражения
равно 2 и достигается при х = 2. Наибольшее же значение функции
равно 2. Равенство значений этих функций может осуществиться только при х = 2. Ответ: 2 Задание 155. Iog2 (4x2 + 1) - Iog2 x = 8x(1 - x). Решение: Преобразуем левую часть уравнения к виду
и достигается при
т. е. наименьшее значение функции
Равенство выполняется только при
Ответ:
Задание 156.
Ответ:
Задание 157. x2 • 2x+1 + 2|x -3|+2 =x2 • 2|x -3|+4 + 2x -1 Ответ:
Задание 158.
Решение: Полагая
получим систему уравнений
Ответ:
Задание 159.
Решение: Из вида уравнения следует, что
т. е. х € [1; 10). Таким образом, сумма 1 + lg х + lg2 х + ... является суммой бесконечно убывающей геометрической прогрессии и равна
Заметим также, что
С учетом этого исходное уравнение преобразуется к виду
получаем уравнение t2 - t - 2 = 0, корни которого t = 2 и t = -1 (последний не удовлетворяет условию t > 0). Из уравнения
т. е. х = 103/4. Ответ:
Задание 160.
Решение: При указанных значениях х суммы 1 + lg x + + lg2 х + ... и 1 - lg х + lg2 x - ... являются суммами бесконечно убывающих геометрических прогрессий и равны соответственно
и
Сумма логарифмов в правой части уравнения преобразуется к виду
Так как
и исходное уравнение преобразуется к виду
Возводя обе части в квадрат и вводя обозначение
получим уравнение 6t2 - t - 1 = 0, имеющее корни
Учитывая, что t > 0, переходим к уравнению
Ответ:
Задание 161.
Ответ: (0; 1); (1; 0) Задание 162.
Ответ: (-2; 0) Задание 163.
Ответ: (4; 4) Задание 164.
Ответ:
Задание 165.
Ответ:
Задание 166.
Ответ: {(9; 7); (9; -7)} Задание 167.
Ответ:
Задание 168.
Ответ: (4; 1) Задание 169.
Ответ: (4; 16) Задание 170.
Ответ: (16; 4) Задание 171.
Ответ: {(1; 1); (3; 9)} Задание 172.
Ответ: {(9; 32/3);(32/3; 9)} Задание 173.
Решение: Так как - ху - 2х + у +
2 = (1 - x)(2 + у), то с учетом соотношений 1 - х > 0, 1 - х # 1 и 2 + у
>0, 2 + у # 1 первое Ответ: (-2; 1) Задание 174.
Ответ:
Задание 175.
Ответ:
Задание 176.
Ответ:
Задание 177.
Ответ: {(3; 10); (-20; 36)} Задание 178.
Ответ: (log9/2 2; 2log9/22) Задание 179.
Ответ: (log4/3 2; 2 log4/32) Задание 180. Решите уравнение
и укажите все решения, входящие в область определения функции
Ответ:
Задание 181. Решите уравнение
Ответ:
Задание 182. Решите систему уравнений
Ответ: (2; 2; 2)
Задание 183.
Решение: Имеем
Ответ:
Задание 184.
Ответ:
Задание 185.
Ответ:
Задание 186.
Ответ:
Задание 187.
Ответ:
Задание 188.
Ответ:
Задание 189.
Ответ: 4 Задание 190.
Ответ: 3 Задание 191.
Ответ: 3 Задание 192.
Ответ: 2 Задание 193. Iog3 5 Iog4 9 Iog5 2 Ответ: 1 Задание 194. lоg2 3 lоg3 4...log9 10 Ответ: Iog2 10 Задание 195. Igtg 3° Igtg 6°...Igtg 87° Ответ: 0 Задание 196. Igtg 1° + Igtg 2° + ... + Ig tg 89° Ответ: 0 Задание 197.
Решение: Учитывая, что
находим
Ответ: 2 Задание 198.
Ответ: 2 Задание 199.
Ответ: 3 Задание 200.
Указание: Учтите, что
Ответ: -3 Задание 201. Найдите Iog2 392, если Iog2 7 = a Решение: Так как 392 = 8 • 49 = 23 • 72, то Iog2 392 = 3 + + 2 Iog2 7 = 3 + 2а. Ответ: 3 + 2а Задание 202.
Ответ:
Задание 203. Найдите Ig308, если Ig 5 = a, Ig 3 = b Ответ:
Задание 204. Найдите Iog3 200, если Iog3 5 = a, Iog2 3 = b Ответ:
Задание 205.
Ответ: а < b Задание 206.
Ответ: а < b Задание 207. a = Iog34 и b = Iog45 Ответ: а > b Задание 208.
Решение: Имеем
но
Значит, a > b. Ответ: a > b. Задание 209.
Решение: Имеем
Ответ: a > b Задание 210.
Ответ: a < b
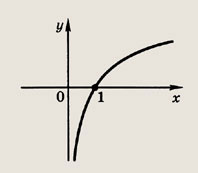
Задание 211. у = 3x Ответ:
Задание 212.
Ответ:
Задание 213. у = Iog2x Ответ:
Задание 214.
Ответ:
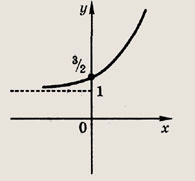
Задание 215. у = 2x-1 + 1 Ответ:
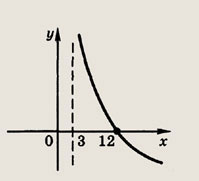
Задание 216. у = -Iog3(x - 3) + 2 Ответ:
Задание 217. y = Iog2|x - 2 Ответ:
Задание 218.
Ответ:
Задание 219.
Ответ:
Задание 220. у = |log2x2| Ответ:
Задание 221. |y| = Iog3 x - 1 Ответ:
Задание 222. |y| = Iog2 (|x| - 2) Ответ:
Задание 223. у = lg (х2 + х - 6) Ответ:
Задание 224. j/ = Iog2 (6x - х2 - 5) Ответ:
Задание 225.
Ответ:
Задание 226.
Ответ:
Задание 227. у = Iog2sin2x Ответ:
Задание 228. у = 3cos x Ответ:
Задание 229.
Ответ:
Задание 230.
Ответ:
• При решении показательных и логарифмических неравенств следует помнить, что функции у = аx и у = loga х (а > 0; а # 1) являются возрастающими при а > 1 и убывающими при 0 < a < 1 на своей области определения. Рассмотрим решения простейших неравенств:
Решите следующие показательные и логарифмические неравенства (231—330): Задание 231.
Ответ:
Задание 232.
Ответ:
Задание 233.
Ответ: (1; 4] Задание 234.
Ответ:
Задание 235.
Ответ:
Задание 236.
Ответ:
Задание 237.
Ответ: [1; 5] Задание 238.
Ответ: (-1; 3) Задание 239.
Ответ:
Задание 240.
Ответ:
Задание 241.
Ответ:
Задание 242.
Ответ:
Задание 243.
Ответ:
Задание 244.
Ответ: (-1; 1) U (2; 4) Задание 245.
Ответ:
Задание 246.
Ответ:
Задание 247.
Ответ:
Задание 248.
Ответ:
Задание 249.
Ответ: (3; 5] Задание 250. 2log2(x + 1)< Iog2(x + 7) Ответ: (-1; 2) Задание 251.
Ответ: (0; 27) Задание 252.
Ответ:
Задание 253.
Ответ:
Задание 254.
Ответ:
Задание 255.
Ответ:
Задание 256.
Ответ:
Задание 257.
Ответ: (1; 2) Задание 258.
Ответ: [2; 4) Задание 259.
Ответ:
Задание 260.
Ответ:
Задание 261.
Ответ: (1; 2) U (2; 3) U и {4} Задание 262.
Ответ: (-5; -4) U {0} Задание 263.
Ответ:
Задание 264.
Ответ:
Задание 265.
Ответ:
Задание 266. 36x - 6x+1 + 8 > 0 Ответ:
Задание 267.
Ответ:
Задание 268.
Ответ:
Задание 269.
Ответ:
Задание 270.
Ответ:
Задание 271.
Ответ:
Задание 272.
Ответ:
Задание 273.
Ответ:
Задание 274.
Ответ:
Задание 275.
Ответ:
Задание 276.
Ответ:
Задание 277.
Ответ:
Задание 278.
Ответ:
Задание 279.
Ответ:
Задание 280.
Ответ: (0; 1) U {5} Задание 281. (logx 2)(log2x 2)lоd24x > 1 Ответ:
Задание 282.
Ответ:
Задание 283.
Ответ:
Задание 284.
Ответ:
Задание 285.
Ответ: [125; 15 625) Задание 286.
Ответ:
Задание 287.
Ответ:
Задание 288.
Ответ:
Задание 289.
Ответ:
Задание 290.
Ответ:
Задание 291.
Ответ:
Задание 292. log1-x(2 + x) < 1 Ответ:
Задание 293. Iog2x(8 - x2) < 1 Ответ:
Задание 294.
Ответ:
Задание 295.
Ответ:
Задание 296.
Ответ: (0, 1) U (2, 6) Задание 297.
Ответ:
Задание 298.
Ответ:
Задание 299.
Ответ:
Задание 300.
Ответ:
Задание 301. |15 - 5 • 2-x | > 4-x* - 6 • 2-x + 13 Ответ:
Задание 302. |4 • 3x - 8| > 9x - 4 • 3x + 7 Ответ:
Задание 303.
Ответ:
Задание 304.
Ответ:
Задание 305.
Ответ:
Задание 306.
Ответ:
Задание 307.
Ответ:
Задание 308.
Ответ:
Задание 309.
Ответ:
Задание 310.
Ответ:
Задание 311.
Ответ:
Задание 312.
Ответ:
Задание 313.
Ответ:
Задание 314.
Ответ:
Задание 315.
Ответ:
Задание 316.
Ответ: {3} Задание 317.
Ответ: {2} Задание 318.
Ответ:
Задание 319.
Ответ:
Задание 320.
Ответ: (-3; -2] U (2; 3) Задание 321.
Ответ: (-2; -1] U (1; 2) Задание 322.
Ответ:
Задание 323.
Ответ:
Задание 324. 1 + Iog2 (x + 10) > log(x-2)(x-4) (х - 2)(x - 4) Ответ:
Задание 325. 1 + Iog0,5 (8 -x)< log(x-1)(x-2) (x + 1)(x - 2) Ответ:
Задание 326.
Ответ: (2; 2,5) U (2,5; 3) Задание 327.
Ответ:
Задание 328.
Решение: При любых
выражение 4-x + 3 • 2x больше 1. Действительно, если
а если х < 0, то 4 -x* > 1. Значит, исходное неравенство может выполняться только при условии
Полагая Iog7 х = t, то данное неравенство сводится к виду
Значения х находим из совокупности решений уравнения Iog7 х = 1, х = 1 и неравенства Iog7 х < 0, откуда х = 7 и x € (0; 1). Ответ: (0; 1) U {7} Задание 329.
Ответ:
Задание 330.
Ответ:
Задание 331.
Решение: Выразим из уравнения
и подставим в неравенство. Получим неравенство
которое выполняется только при х = 0. Отсюда х = 0; у = -2,5. Ответ:
Задание 332.
Ответ: {(0; 1); (0; -1)} Задание 333.
Ответ:
Задание 334.
Ответ:
Задание 335.
Ответ: {(-2; -2); (4; -2)} Задание 336.
Ответ: {(-4; 4); (7; 4)} Задание 337. Найдите все значения x, для которых величина
удовлетворяет уравнению
Ответ:
Задание 338. Найдите все значения х, для которых величина
удовлетворяет уравнению
Ответ:
Задание 339.
Ответ:
Задание 340.
Ответ:
Задание 341.
Ответ:
Задание 342.
Ответ:
Задание 343. (2x + 2а - 1) (а + 1 - 2x) = 0 Ответ:
Задание 344. (2-x + Зс + 4) (5 - с - 2-x) = 0 Ответ:
Задание 345.
Ответ:
Задание 346.
Ответ:
Задание 347.
Ответ: При
при а € (-1; 9] => х1 = 9, х2 = 99, x3 = а; при а € (9; 99] => x1 = 99, x2 = а; при
Задание 348.
Ответ: при
при с € (-9; 0] => x1 = 3, х2 = 75, х3 = с + 3; при с € (0; 72] => x1 = 75, х2 = с + 3; при
Задание 349.
Решение: Полагая 3x = t > 0, переходим к уравнению t2 - 2at — 4 + 4a =0, корни которого t1 = 2 и t2 = 2а — 2. Из соотношения t = 3x = 2 получаем х = Iog32 при любых
Во втором случае, когда 3x = 2а -2, решение возможно лишь при а > 1 и х = = Iog3(2a - 2), откуда и получаем ответ. Ответ: при
при
Задание 350. 16-x -4b • 4-x = 76 + 6 Решение: Полагая 4-x = t, переходим к уравнению t-2- 4bt - 7b - 6 = 0, откуда
Решение существует только при тех b, когда t1 или t2 положительны. Решив неравенство
находим
Неравенство
не выполняется ни при каких b. Отсюда и получаем ответ. Ответ: при
При
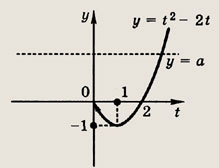
Задание 351.
Решение: Полагая 2x = t > 0, получим уравнение
сводящееся к квадратному уравнению t2 - 2t - а = 0, t # 1, корни которого
Чтобы удовлетворялось условие t > 0, мы должны были бы решить иррациональные неравенства, позволяющие найти соответствующие значения а, но гораздо удобнее воспользоваться другим методом рассуждений. Разрешим уравнение t2 - 2t - а = 0 относительно параметра а, т. е. а = t2 - 2t, и рассмотрим в координатах (t; у) графики функций у = t2 - t, где
решений нет, при а € (-1; 0) существуют два положительных решения
только одно положительное решение
Ответ:
при
при
Задание 352.
Ответ: при
при
при
Задание 353. alg2(x2 + 10) + 2lg(x2 + 10) + 8а = 0 Решение: Положим
и получим уравнение at2 + 2t + 8a = 0, откуда
Значения а можно найти, решив неравенство
что, вообще говоря, не просто. Гораздо удобнее, выразив а из квадратного уравнения, построить графики функций
Так как t1 и t2 являются абсциссами точек пересечения этих линий, то из расположения графиков этих функций легко находим те значения а, при которых существуют значения t1 и t2 соответствующие им значения х. Ответ: при
при
при
при
Задание 354.
Ответ: при
при
Задание 355. Iog3 cos х - Iog4 cos х - Iog9 cos x = a - 1 Ответ: при
при
Задание 356.
Ответ: при
при
Задание 357. -0,5 + logb-3 (sin 2x) = logb-3(cos x) Ответ: при
при
Задание 358. 2 + Iogb+3(sinx) = logb+3(sin 2x) Ответ: при
при
Ответ: при
при
Задание 360. 4sin x -a - 3 = (a + 2) • 2sin x Ответ: при
при
Задание 361.
Ответ: при
при
при
Задание 362.
Ответ: при
при
Задание 363.
Ответ: при
при
при
при
Задание 364.
Ответ: при
при
Задание 365.
Решение: Из исходного уравнения следует, что
Для существования решений этого уравнения необходимо, чтобы
При выполнении этого условия уравнение превращается в совокупность двух уравнений: 3-c - 23 = = 6x - 5 - х2 и 3-c - 23 = -6x + 5x + x2. С учетом того, что дискриминанты в этих уравнениях должны быть неотрицательны, получаем ответ. Ответ: при
при
при
Задание 366. Iog3 (31 - |x2 - 6x + 5|) = c Ответ: при
при
при
Задание 367. Iog4(x - 5) = -Iog0,25(|a - x| - 3) Решение: Учитывая, что
получаем уравнение х - 5 = |а - ч| - 3, т. е. ч - 2 = |а - ч|. Так как х > 5, то левая часть уравнения положительна и уравнение распадается на совокупность двух уравнений: х - 2 = а - х и х - 2 = х - а. Из первого находим
получаем a > 8. Второе
уравнение выполняется при любом х > 5, если a = 2, а при других Ответ: при
при
при
Задание 368. Iog3(6 - x) = 2 log9(3 - |6 - x|) Ответ: при
при
Задание 369. logd(4x + d) = logd (x2 - 4) Ответ: при
при
при
Задание 370. loga(a + 5x) = loga (x2 - 6) Ответ: при
при
при
Задание 371.
Ответ: при
при
Задание 372.
Ответ: при
при
Задание 373.
Ответ: при
при
при
Задание 374.
Ответ: при
при
при
при
Задание 375.
Ответ: при
Задание 376.
Ответ: при
при
Задание 377.
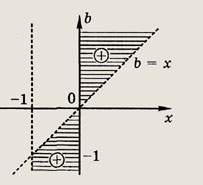
Решение: Так как
то задача сводится к решению неравенства
Для решения этого неравенства на координатной плоскости (х; b) найдем области, где выражение, стоящее в левой части неравенства, сохраняет знак и определим его. Границы этих областей задаются соотношениями x + 1 > О, х + 1 = 1, т. е. х = 0 к b = х. На рис.
заштрихованы те области, координаты точек которых удовлетворяют неравенству. Отсюда и вытекает окончательный результат. Ответ: при
при
при
Задание 378.
Ответ: при
при
при
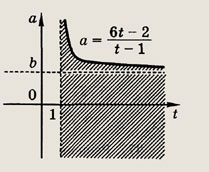
Задание 379.
Решение: Положим
и рассмотрим полученное неравенство (а - 6)t < а - 2. На координатной плоскости (t; а) изобразим области, координаты точек которых удовлетворяют этому неравенству. Границы этих областей определяются соотношениями t = 1 и (а - 6)t — а - 2 или
На рис.
нужная нам область заштрихована. Отсюда при
и при
Учитывая, что
получаем окончательный результат. Ответ: при
Задание 380.
Ответ: при
при
при
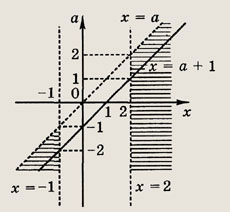
Задание 381.
Решение: На координатной а х = а
плоскости (х; а) изобразим области, в которых левая часть неравенства сохраняет
знак. Границы областей определяются соотношениями x + 1 = 0, х - а = 1, х -
2 = 0, х - а > 0. На
области, где левая часть положительна, заштрихованы. Границы, координаты точек которых не удовлетворяют неравенству, изображены пунктиром. Следует учесть, что при переходе через границу а = х - 1 выражение Iog23 (х - а) знак не меняет. Отсюда получаем ответ. Ответ: при
при
при
Задание 382.
Ответ: при
при
при
при
при
Задание 383.
Ответ: при
при
при
при
Задание 384.
Решение: Перейдем в исходном неравенстве к основанию 2 и получим неравенство
Если
т. e.
то получаем
откуда
Аналогично рассматриваем оставшиеся случаи
Ответ: при
при
при
Задание 385.
Ответ: при
при
при
Задание 386.
Решение: После несложных преобразований придем к неравенству
Поскольку х < 3, при таких значениях x имеем 12 — 11x-2 > 0 и неравенство сводится к виду
откуда получаем окончательный результат. Ответ: при
при
Задание 387.
Ответ: при
при
Задание 388.
Ответ: при
при
при
при
при
Задание 389. loga (x2 + 4x - 1) < Iog2a (x2 + 4x - 1) Решение: Переходя к основанию 2, преобразуем неравенство к виду
Если
Ответ: при
при
Задание 390. logx+a+2(2x + a) < 1 Ответ: при
при
при
Задание 391.
Ответ: при
при
Задание 392.
Ответ: при
при
Задание 393.
Решение: Исходное неравенство сводится к системе неравенств первое из которых выполняется для любых х € R, а для двух других это условие будет реализовано при значениях b, удовлетворяющих следующей системе неравенств:
Ответ:
Задание 394.
Ответ:
Задание 395.
Ответ:
Задание 396.
Ответ: а € (-3; -1) и (2; 4) Задание 397. a • 9x + 4(a - 1) • 3x + a > 1 Ответ:
Задание 398. (а - 3) • 4x - 8 • 6x + (а + 3) • 9x = 0 Ответ: а € (-3; 5] Задание 399.
Решение: Положим
и перейдем к неравенству
Из условия
получаем, что функция имеет минимум при t = 1, а значение функции при t = 1 равно 2. Отсюда вытекает, что при
неравенство имеет хотя бы одно решение. Ответ:
Задание 400. loga+x х(а - х) < loga+x х Ответ:
Задание 401. При каких а уравнение
не имеет решений? Ответ:
Задание 402. При каком с € R уравнение
Решение: Введем обозначение 3-x = t > 0 и перейдем к уравнению t2 - (с + 2)t + (1 - с)(2с + 1) = 0, корни которого t1 = 2с + 1 и t2 = 1 - с. Уравнение имеет единственное решение, когда t1 и t2 имеют разные знаки, т. е.
Ответ:
Задание 403. При каком а € R уравнение
Ответ:
Задание 404. Найдите все а, при которых уравнение
Ответ:
Задание 405. Найдите все а, при которых неравенство 56 • 3x > 9x - а не имеет ни одного целочисленного решения. Ответ:
Задание 406. Найдите все значения а из интервала (2; 5), при каждом из которых существует хотя бы одно х € [2; 3], удовлетворяющее уравнению
Решение: Рассматривая возможные значения функций в левой и правой частях равенства, легко заметить, что
и равенство возможно только при выполнении условий
Первое из этих уравнений при х € [2; 3] имеет единственное решение
Значения a € (2; 5) находим, решив уравнения
откуда получаем
Ответ:
Задание 407. Найдите сумму всех значений параметра а из интервала (2; 7), при каждом из которых существует хотя бы одно х € [1; 2], удовлетворяющее уравнению
Ответ:
Задание 408. При каких значениях b наименьшее значение функции у = Iog2 (1 + 3 sin2 х) [Iog2 (1 + 3 sin2 х) - b - 1] -- b2 + 3b + 7 равно 2? Ответ:
Задание 409. При каких значениях d наименьшее значение функции
не меньше (-1)? Ответ:
Задание 410. При каких значениях а периметр фигуры, заданной на координатной плоскости условием:
Ответ:
Задание 411. Найдите все а и b, при которых наибольшее значение функции
Ответ:
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
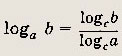
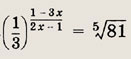
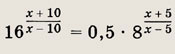
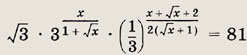
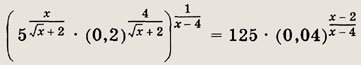
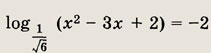
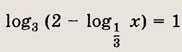
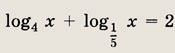
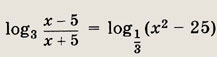
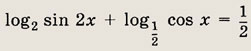
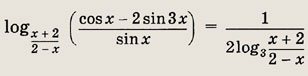
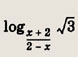

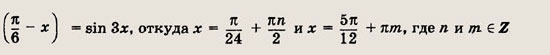
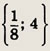

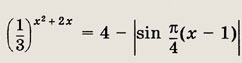
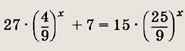
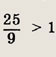
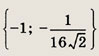
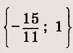

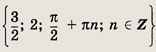
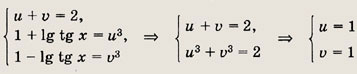
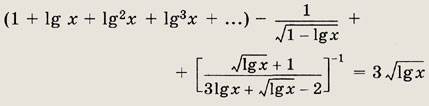
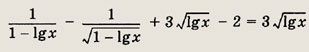
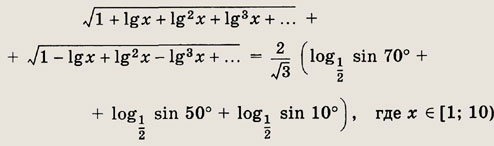
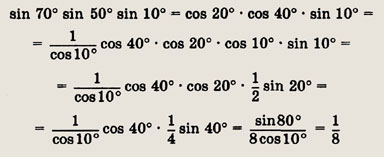

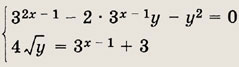
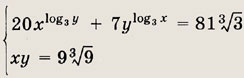
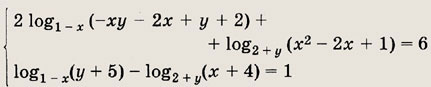
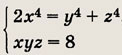
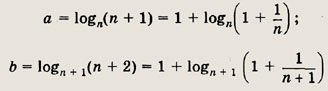

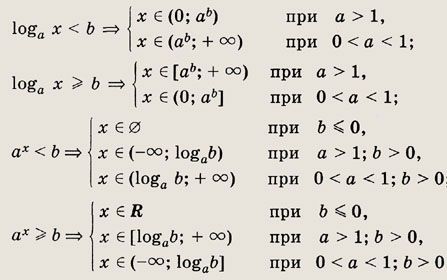
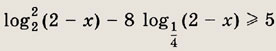

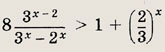
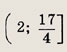
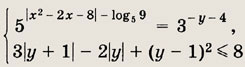
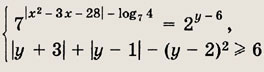
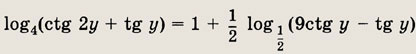
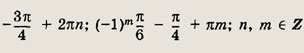
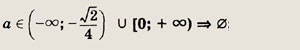
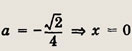
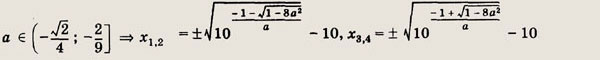
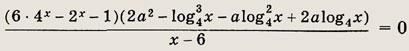
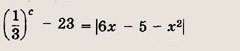
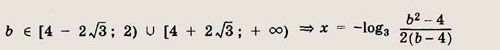
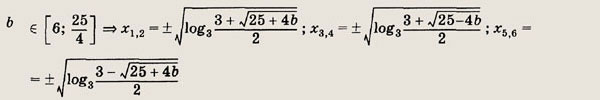
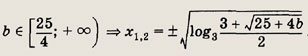
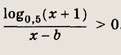
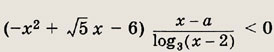
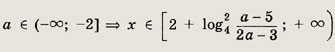
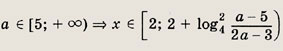
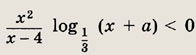
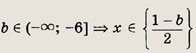
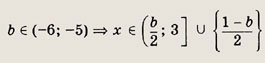
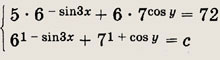
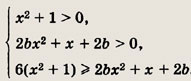
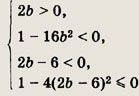
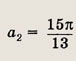
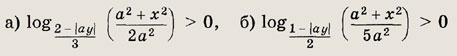
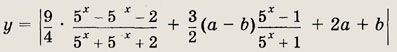
 Главная
Главная