Квадратное уравнение.
График квадратного трехчлена
то числа
Если D < 0, то квадратное уравнение корней не имеет. Справедливы формулы:
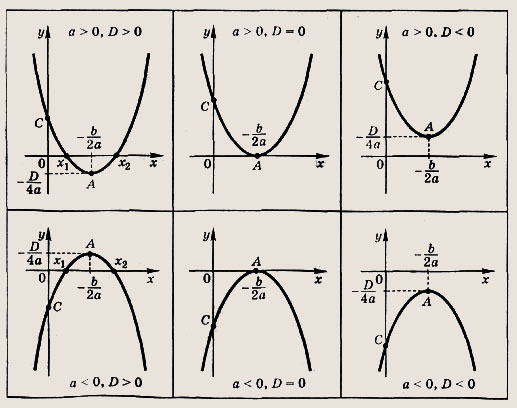
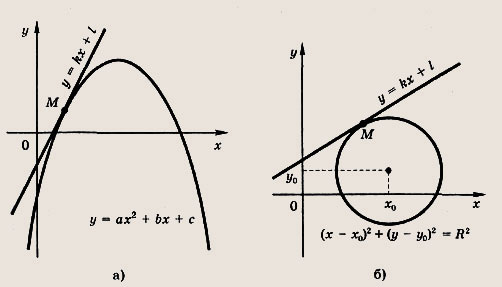
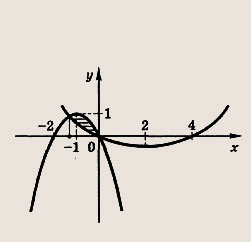
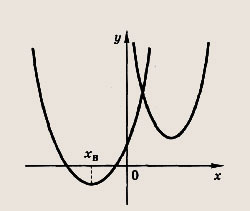
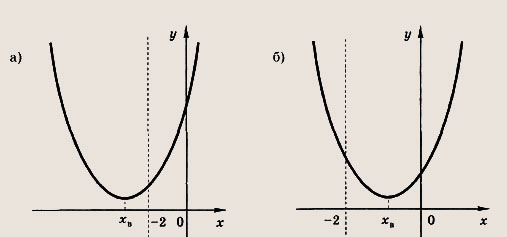
— формулы Виета; а ах2 + bх + с = а(х - х1)(х - х2) — формула разложения на множители. Графиком квадратичной функции (квадратного трехчлена) у = ах2 + bх + с является парабола. Расположение параболы в зависимости от знаков коэффициента а и дискриминанта D приведено на рис.
Числа х1 и х2 на оси абсцисс — корни квадратного уравнения ах2 + bх + + с = 0; координаты вершины параболы (точки А) во всех случаях
точка пересечения параболы с осью ординат имеет координаты (0; с). Подобно прямой и окружности парабола разбивает плоскость на две части. В одной из этих частей координаты всех точек удовлетворяют неравенству у > ах2 + bх + с, а в другой — противоположному. Знак неравенства в выбранной части плоскости определяем, найдя его в какой-либо точке этой части плоскости. Рассмотрим понятие касательной к параболе (или окружности). Прямую у - kx + 1 назовем касательной к параболе (или окружности), если она имеет с этой кривой одну общую точку.
В точке касания М(х; у) для параболы выполняется равенство kx +1 = ах2 + bх + с (для окружности — равенство (х - х0)2 + (kx + 1 - у0)2 - R2). Приравнивая дискриминант полученного квадратного уравнения нулю (так как уравнение должно иметь единственное решение), приходим к условиям для вычисления коэффициентов касательной. Решите следующие квадратные и сводящиеся к квадратным после простых преобразований уравнения (1—19): Задание 1. х2 - 6х + 8 = 0 Ответ: {2; 4} Задание 2. 6х2 - 1х + 1 = 0 Ответ:
Задание 3. 5х2 - 1 = 0 Ответ:
Задание 4. Зх - 2х2 = 0 Ответ:
Задание 5. х2 + 6x - 10 = 0 Ответ:
Задание 6. -х2 + 5х - 7 = 0 Ответ:
Ответ:
Задание 8.
Ответ:
Ответ: {4; 5} Задание 10.
Указание: х = 2 не входит в ОДЗ уравнения. Ответ: 3 Задание 11.
Указание: х = +6 не входит в ОДЗ уравнения. Ответ:
Задание 12.
Ответ: 1 Задание 13.
Ответ: {-5; 1} Задание 14.
Ответ: {-2; -1} Задание 15.
Ответ: 2 Задание 16.
Ответ:
Задание 17.
Ответ: {-4; 9} Задание 18. (х + З)3 - (х + 1)3 = 56 Ответ: {-5; 1} Задание 19. (х - 2)3 - (х - З)3 = 19 Ответ: {0; 5} Решите уравнения 20—40, сводящиеся к квадратным после подходящей замены: Задание 20. (х2 + х - 1)(х2 + х + 2) = 4 Решение: Выполнив замену х2 + х = у, сводим данное уравнение к квадратному у2 + у - 6 = 0, откуда у1 = -3; у2 = 2. Теперь остается решить уравнения х2 + х + 3 = 0, х2 + х - 2 = 0. Первое из них решений не имеет. Решения второго — числа х = -2; х = 1 Ответ: {-2; 1} (х2 + 3х+ 1)(х2 + 3х-3) = 5 Ответ: {-4;-2;-1; 1} Задание 22. х(х - 1)(х - 2)(х - 3) = 15 Указание: Сначала перемножьте скобки (х - 3) и (х - 1)(х - 2), затем сделайте замену, полагая х2 - Зх = у. Ответ:
Задание 23.
Ответ:
Задание 24. 2(х2 + х +1)2 - 7(х - 1)2 = 13(х3 - 1) Решение: Так как х3 - 1 = (x2 + x + 1) (x - 1), a
ни при каком х, то, разделив обе части данного уравнения на (х2 + х + 1)2 и полагая
приходим к уравнению 7у2 + 13у -2 = 0, откуда
Ответ:
Задание 25. (х + З)2 + 7(х2 - 9) + 6(х - З)2 = 0 Ответ:
Задание 26. (х - 2)2(х + 1)2 - (х - 2)(х2 - 1) - 2(х - 1)2 = 0 Решение: Число х = 1 не является решением данного уравнения. Поэтому, поделив обе его части на (х - 1)2, приходим к равносильному уравнению
равен либо 2, либо (-1). Решая полученные квадратные уравнения, находим их корни. Ответ:
Задание 27.
Ответ:
Задание 28.
Решение: Запишем уравнение в виде
т. е.
либо х2 + 5х - 6 = х2 - 5х + 6 т. е.
Ответ:
Указание: Упростите каждую дробь, разделив числитель на знаменатель. Ответ:
Задание 30.
Ответ:
(х2- 6х)2-2(х - 3)2 = 81 Указание: Воспользуйтесь тем, что х2 - 6х = (х - З)2 - 9, и положите у = (х - З)2. Ответ:
Задание 32. (х2 + 2х)2 - (х + 1)2 = 55 Ответ: {-4, 2} Задание 33.
Указание: Положите
Ответ:
Задание 34.
Указание: Положите
Ответ:
Задание 35.
Решение: Поделив числитель и знаменатель каждой из дробей на х и обозначив
приходим к уравнению
Ответ:
Задание 36.
Ответ:
(х2 -6x- 9)2 = x(x2 - 4x- 9) Указание: Сделайте замену
Ответ:
Задание 38. х(х2 + 1) - 2(х2 -х + 1)2 Решение: Перепишем уравнение в виде
приходим к уравнению 2у2 = у + 1 Отсюда у = 1 и
Теперь решаем уравнения
Ответ: {1} Задание 39.
Указание: См. решение задания 40. Ответ:
Решение: Запишем уравнение в виде
получаем квадратное уравнение у2 - 4у - 12
= 0
и
Ответ:
Задание 41. Осенью закупили картофель на сумму 810 р. Весной 1 кг картофеля стал стоить на 1 р. дороже, чем осенью. Поэтому на ту же сумму весной было куплено на 27 кг картофеля меньше. Сколько стоил 1 кг картофеля весной? Ответ: 6 р. Задание 42. Зарплата служащего до повышения составляла 700 р. Она повышалась дважды, причем процент повышения зарплаты во второй раз был вдвое больше, чем в первый. На сколько процентов была повышена зарплата в первый раз, если после двух повышений она составила 924р.? Ответ: На 10 % Задание 43. В результате переоборудования производительность завода за первый год возросла на m% , а за второй — на 5% больше, чем за первый. В результате за два года производительность завода увеличилась на 38%. На сколько процентов увеличилась производительность за первый год? Ответ: На 15 % Задание 44. Один из корней уравнения 5х2 - ах + 12 = 0 на 1,4 больше другого. Найдите значения коэффициента а. Указание: Воспользуйтесь теоремой Виета. Ответ:
Задание 45. Один из корней квадратного уравнения 2х2 - 14х + с = 0 в 2,5 раза больше другого. Найдите коэффициент с. Ответ: {20} Задание 46. Один из корней квадратного уравнения х2 -- (а + 6)х + а2 = 0 равен 2. Найдите а. Ответ: {- 2; 4} Задание 47. Найдите значения коэффициента а, при которых корни уравнения (2а - 5)х2 - 2(а - 1)х + 3 = 0 равны между собой. Ответ: {4} Задание 48. Пусть x1 и х2 корни уравнения х2 + ах + 4 = 0. Не вычисляя x1 и x2, найдите значения следующих выражений: a) x1х2 б) (x1 + 1)(х2 + 1) в) x12 + x22 г) Решение д): Согласно теореме Виета получаем x1 + х2 = -а, x1х2 = 4. Тогда x13 + х23 = (x1 + х2)[(x1 + х2)2 - 3x1х2] = -а(а2 - 12) = 12а - а3 Ответ: а) 4 б) 5 - а в) а2 - 8 г) Задание 49. Квадратное уравнение х2 + Зх - 5 = 0 имеет корни x1 и x2. Составьте квадратное уравнение, имеющее следующие корни: а) 2х1 и 2х2 б) - х1 и - х2 г) x12 и x22 Решение г). Имеем x1 + x2 = -3, x1x2 = -5. Тогда x12 + x22 = (x1 + x2)2 -2x1x2 = 19 x12 x22 = (-5)2 = 25 Поэтому, применяя теорему Виета, записываем уравнение, имеющее корни x12 и x22 , и получаем х2 - 19х + 25 = 0 Ответ: а) х2 + 6х - 20 = 0 б) х2 - Зх - 5 = 0 в) х2 + 8х +
15 = 0 Задание 50. Найдите все значения а, при которых сумма корней квадратного уравнения х2 - 2а(х - 1) - 1 = 0 равна сумме квадратов его корней. Ответ:
Задание 51. При каких значениях а разность корней уравнения 2х2 - (а + 1)х + а - 1 =0 равна их произведению? Решение: Корни данного уравнения — это числа x1 = 1,
откуда а = 2. Ответ: 2 Задание 52. При каких значениях а уравнения х2 + ах+1 = 0 и х2 + х + а = 0 имеют общий корень? Решение: Для переменных х и а должны одновременно выполняться равенства
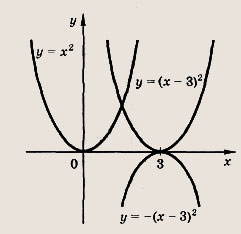
ах - х +1 - а = (а - 1)(х - 1) = 0 Если а = 1, то уравнения совпадают, но не имеют решений. Если же х = 1, то, подставляя это значение в любое уравнение, находим а = -2. Ответ: -2 Постройте графики заданных функций. На координатной плоскости отметьте штриховкой множество точек, координаты которых удовлетворяют указанным неравенствам (53—64): Задание 53. у = х2, у = (х - З)2, у = - х2 + 6х - 9 Ответ:
Задание 54.
Ответ:
Задание 55.
Ответ:
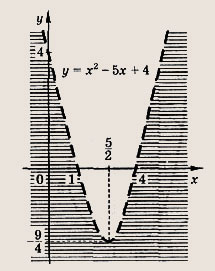
Задание 56. у = х2 - 5х + 4, у < х2 - 5х + 4 Ответ:
Ответ:
Задание 58.
Ответ:
Ответ:
Ответ:
Задание 61.
Ответ:
Задание 62.
Ответ:
Задание 63.
Ответ:
Задание 64.
Ответ:
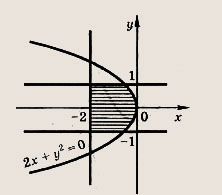
Задание 65. Фигура Ф состоит из точек М(х; у) таких, что неравенство
выполняется при всех значениях параметра t. Постройте фигуру Ф и найдите ее площадь. Ответ: Решение: Из условия следует: дискриминант квадратного трехчлена (относительно переменной t) z = t2 + 2tx + 4t - у2 не положителен. Получаем:
т. е.
Значит, множество Ф — это круг радиуса 2 с центром в точке А (2, 0)
Его площадь
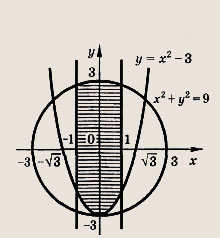
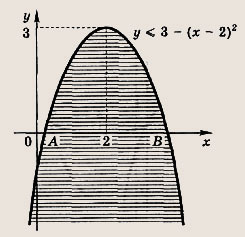
Задание 66. Фигура Ф состоит из точек М(х; у) таких, что неравенство
выполняется для всех значений параметра t. Постройте фигуру Ф и найдите длину отрезка оси абсцисс, лежащего внутри фигуры Ф. Указание: См. решение задания 65. Ответ:
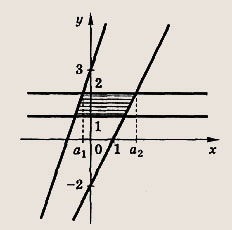
При решении задач 67—70 существенно помогает штриховка в плоскости (х; а) областей, задаваемых неравенствами, входящими в условия этих задач. Задание 67. Найдите все значения а, при которых система неравенств
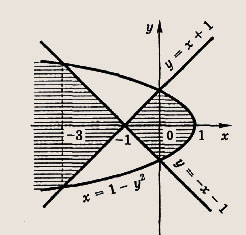
имеет единственное решение. Решение: В плоскости (х, у) отметим штриховкой множество точек, удовлетворяющих указанным неравенствам. Мы видим, что параболы а = -х2 - 2х и
пересекаются только в точках
Поэтому заштрихованная область пересекается с прямой а = const в одной точке только при а = 0 и а = 1. Ответ: {0; 1} Задание 68. При каких значениях а система
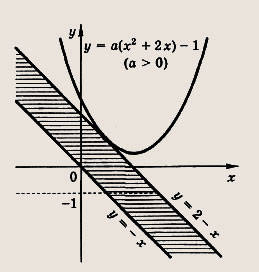
имеет единственное решение? Решение: В плоскости (х, у) отметим штриховкой множество точек, удовлетворяющих неравенству (у + х)(у + х - 2) < 0
Очевидно, что если а = 0, то система имеет бесконечно много решений: (х; -1), где
Если же а #0, то система имеет единственное решение только в том случае, если прямая у = 2 - х служит касательной к параболе у = ах2 + 2ах - 1 при а > 0, либо прямая у = -х служит касательной к той же параболе, но при а < 0. Рассмотрим эти случаи. Прямая у = 2 - х — касательная к параболе у = ах2 + 2ах - 1 в том и только том случае, если уравнение ах2 + 2ах - 1 = 2 - х имеет единственное решение. Имеем ах2 + 2(а +1)х — 3 = 0; D = (2а + 1)2 + 12а = 4а2 + 16а + 1 Приравнивая дискриминант нулю, получаем решения
Но оба эти значения отрицательны и, следовательно, не подходят. Теперь ищем значения а < 0, при которых прямая у = - х касается параболы у = ах2 + 2ах - 1 Проведя вычисления, получаем
Ответ:
Задание 69. Решите систему неравенств
Указание: См. решение задания 70. Ответ: При
при
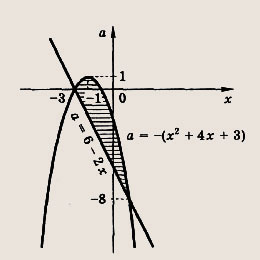
Решите систему неравенств
Решение: В плоскости (х; а) отметим штриховкой область, где выполнены оба неравенства
На прямой 2х + а + 6 = 0 имеем
На параболе а = -(х2 + 4х + 3) получаем,
— ее правую половину. Ответ: При
при
при
Решение задач 71—92 облегчает построение графиков входящих в условия задач квадратных трехчленов при различных значениях параметров. Задание 71. При каких а неравенство (а + 4)х2 - 2ах + а - 6 < 0 выполнено для всех
Указание: Здесь должны выполняться неравенства а + 4 < 0 и D <0. Ответ:
Задание 72. При каких а неравенство
Решение: Так как х2 - Зх + 4 > 0 при всех х € R, то исходное неравенство равносильно неравенству 2х2 - (а + 3)х + 2 > 0 Последнее справедливо при всех
в двух случаях: либо D = (а + З)2 - 16 < 0, т. е. а € (-7; 1) — в этом случае неравенство справедливо вообще для всех х е R
либо при D > 0 оба корня должны быть отрицательными. Положим у = 2х2 - (а + 3)х + 2. Тогда сформулированное условие равносильно выполнению системы
Объединяя два рассмотренных случая, получаем, что a < 1. Ответ:
Задание 73. При каких а неравенство (х - За) (х - а - 3) < 0 выполнено для всех
Указание: См. решение задания 74. Ответ:
Задание 74. При каких а неравенство
Решение: В плоскости (х; а) отметим штриховкой нужную область
Любое
лежит в заштрихованной области при a1< а < а2, где a1 — корень уравнения 4а + 3 = 2, т. е.
а а2 — корень уравнения 2а - 2 = 1, т. е.
Ответ:
Задание 75. При каких а число 3 заключено между корнями уравнения х2 - 2ах + а2 - 1 = 0? Указание: Пусть у2 = х2 - 2ах + а2 - 1 Тогда условие задачи равносильно выполнению неравенства D > 0, у(3) < 0. Ответ:
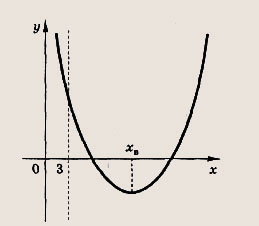
Задание 76. При каких а оба корня уравнения х2 - 6ах + 9а2 - 2а + 2 = 0 больше 3? Решение: Положим у - х2 - 6ах + 9а2 - 2а + 2, хB = За — абсцисса вершины этой параболы
Тогда условие задачи равносильно выполнению неравенств хB = За >
3, у(3) = 9 - 18а + 9а2 - 2а + 2 = 9а2 - 20а + 11 >
0, D = 2а - 2 > 0.
Задание 77. При каких а корни уравнения х2 - (а - 1)х + 2а --1 = 0 имеют разные знаки и оба принадлежат отрезку [- 2; 2]? Указание: См. решение задания 78. Ответ:
Задание 78. При каких а корни уравнения х2 - 2(а - 1)х + 2а + + 1 = 0 имеют разные знаки и оба по модулю меньше 4? Решение: Рассмотрим функцию у = х2 - 2(а - 1)х + 2а + 1
Тогда условие задачи равносильно выполнению неравенств
откуда получаем, что
Ответ:
Задание 79. При каких а среди решений неравенства х2 - 37х < а нет ни одного целочисленного решения? Ответ:
Задание 80. При каких а неравенство 18х > х2 + а не имеет ни одного четного целочисленного решения? Указание: Рассмотрите график функции у = х2 -- 18х + а при различных а. Ответ:
Задание 81. При каких а наибольшее значение функции у = -х2 + 2ах - 71 на
равно 10? Указание: См. решение задания 82. Ответ: {-15; 9}. Задание 82. При каких а наименьшее значение функции у = х2 - 2ах + 43 на
равно 7? Решение: Рассмотрим два возможных варианта
расположения вершины параболы: 1) хB - а < -2. Тогда наименьшее значение функции у = х2 - 2ах + 43 достигается в точке х = -2. Имеем у(-2) = 4а + 47 = 7, откуда а = -10; 2)
Ответ: {-10; 6}. Задание 83. При каких а наибольшее значение функции у = х2 - Зах + а2 на [-1; 3] равно 5? Указание: См. решение задания 84. Ответ:
Задание 84. При каких а наименьшее значение
функции на [-3; 1] равно 8? Решение: Если абсцисса вершины параболы
у = -х2 + 4ах + + 5а2, т. е. хB = 2а, удовлетворяет
условию 2а < -1, то наименьшее значение функции у = -х2 + 4ах
+ 5а2 на [-3; 1] достигается при х = 1.
Ответ:
Задание 85. Найдите наибольшее значение функции у = -2х2 - ах + 3 на отрезке [1;2]. Ответ: Задание 86. Найдите наименьшее значение функции у = Зх2 + ах - 5 на отрезке [-1; 3]. Решение: Рассмотрим три случая. 1) Если
то наименьшее значение функции у = Зх2 + ах — 5 на [—1; 3] равно у(— 1). Значит, при
то наименьшее значение этой функции на [-1; 3] достигается в вершине параболы, т. е. при
и оно равно
Таким образом, при
т. е. а < -18, то наименьшее значение функции у = Зх2 + ах - 5 на [-1; 3] составляет с у(3) = 22 + За. Ответ: при Задание 87. Функция
определена на отрезке [5; 7]. Найдите все значения а, при которых наибольшее значение f(x) на [5; 7] не превышает 0,1. Указание: См. решение задания 88. Ответ:
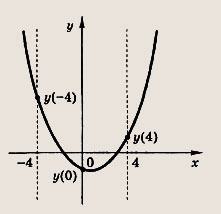
Задание 88. Функция
определена на отрезке [-7; -4]. При каких значениях а наибольшее значение f(x) на [-7; -4] не превышает 0,5? Решение: Построим график функции у = х2 + 6х + а = (х + З)2 + + а - 9 и найдем те значения а, при которых параболы пересекают ось абсцисс в точках х = -4 и х = —1. Получаем а = 8 и а = -7. Далее рассмотрим два случая. 1) Если а < -7, то значения у = х2 + 6х + а на [-7; -4], отрицательны, а тогда для f(х) = у-1(х) выполнено условие задачи. 2) Если же а > 8, то наименьшее значение у = х2 + 6x + а на [-7, -4] равно ,у(-4) = а - 8. Для того чтобы
на [-7; -4], должно выполняться условие
т. е.
Ответ:
Задание 89. При каких значениях а функция
Указание: См. решение задания 90. Ответ:
Задание 90. При каких значениях а функция Решение: Для выполнения условий задачи функция у = х2 + 4х + 20 = (х + 2)2 + 16 должна возрастать на отрезке [За; а + 3]. Значит, этот отрезок должен лежать
Получаем неравенства
Отсюда
Задание 91. Найдите все а, при которых корни уравнения х2 + 2х - а2 + 1 = О лежат между корнями уравнения х2 + 2(а + 1)х + а(а - 1) = 0. Решение: Корни уравнения х2 + 2х - а2 + 1 = 0 — это числа х1 = -1+ а, х2 = -1 - а. Рассмотрим функцию у = х2 + 2(а + 1)х + а(а + 1) Для того чтобы выполнялось
требование задачи, необходимо и достаточно выполнения условий Ответ:
Задание 92. При каких а корни уравнений х2+ 4х - 5 = 0 и х2+ах + а2-а-9 = 0 образуют арифметическую прогрессию? Решение: Корнями уравнения х2
+ 4х - 5 = 0 являются числа х1 = -5; Х2 = 1. Таким образом,
эти числа и корни уравнения х2 + ах + + а2 -а-9 = 0 образуют
арифметическую прогрессию только в том 1) -17 и -11; Подставляя каждое из этих чисел в уравнение, находим допустимые значения а. Решение получается только для третьей пары чисел и только при а = 4. Ответ: {4} Задание 93. Найдите все а, при которых существуют такие числа х и у, что х2 + 2у2 + а2 + ху - ах + ау = 3 Указание: См. решение задания 94. Ответ:
Задание 94. Найдите все а, при которых существуют такие числа х и у, что х2 + 8у2 + 4а2 - 2ху + 2ах + 4aу = 12 Решение: Запишем уравнение в виде
х2 - 2(у - а)х + 8у2 + + 4а2 + 4ау - 12 =0.
Для того чтобы это квадратное уравнение имело решения при каких-либо у и а,
нужно, чтобы его дискриминант был
т. е.
т. е. 12а2< 84. Отсюда получаем
Ответ:
Задание 95. При каких значениях параметра а уравнение х4 + 2ах2 -За -2 = 0 имеет четыре различных корня, причем два из них меньше (-1), а два других меньше
Решение: Требования задачи будут выполнены, если функция у = t2 + 2at - За - 2 будет иметь два различных корня, принадлежащих интервалу (1; 2). Для этого должны выполняться следующие условия:
т. е.
у(1) = -а - 1 > 0, т.
е. а < -1;
откуда
Ответ:
Задание 96. При каких а сумма корней уравнения х2 + 2(а2 - За)х - (6а3 - 14а2 + 4) = 0 принимает наибольшее возможное значение? Решение: Для того чтобы уравнение имело корни должно выполняться неравенство
откуда либо
либо
При этих значениях параметра а нужно найти наибольшее значение величины S(a) = 6a - 2a2 - суммы корней этого уравнения. Легко видеть, что это наибольшее значение достигается при a = 1. Ответ: {1}
|
Полезные публикации |
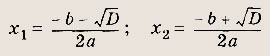
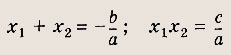
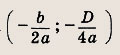
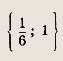
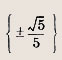
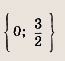
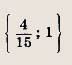
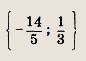

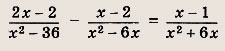
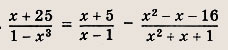
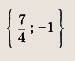
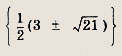

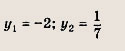
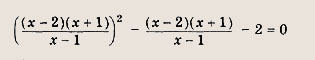
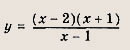
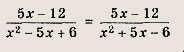
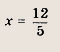
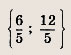
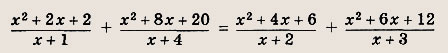

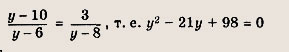
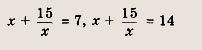
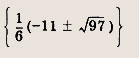

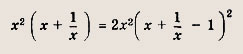
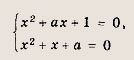

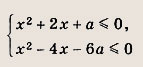
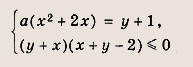
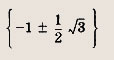
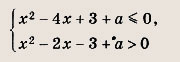
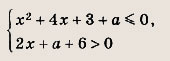
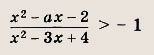
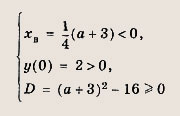
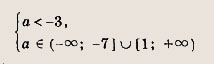
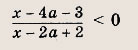
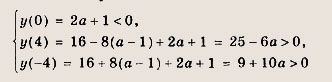
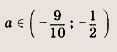
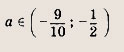
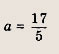
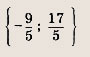
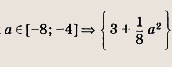
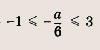
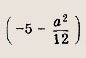
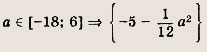
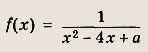
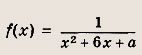
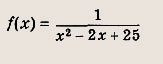
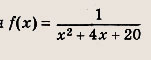
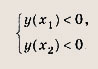
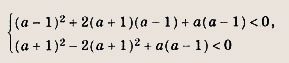
 Главная
Главная