Многочлены. Уравнения
высших степеней, системы уравнений
называется многочленом степени
числа а0, а1; ..., аn — коэффициентами многочлена. Всякий многочлен М(х) можно поделить с остатком на многочлен N(x), т. е. получить равенство М(х) = Q(x)N(x) + R(х). Здесь Q(x) и R(х) — также некоторые многочлены: Q(x) — частное, а R(х) — остаток от деления М(х) на N(x). При этом степень остатка R(х) строго меньше степени делителя N(x). В частности, если N(x) = х - с, то М(х) = (х - c)Q(x) + b, где число b равно М(с), т. е. остаток отделения многочлена М(х) на (х - с) равен М(с) (теорема Безу). Если М(с) = 0, то число с называется корнем многочлена М(х). Пусть М(х) - - многочлен степени n, а х = с1 — его корень; тогда М(х) = (х - c1)Q(x), где Q(x) имеет степень (n - 1). Если же известны n корней с1; ..., сn многочлена М(х), то М(х) = а0(х - x1)(x - х2) ... (х - хn), где а0 — коэффициент при старшей степени многочлена М(х) (старший коэффициент). Разделите «углом» многочлен М(х) на многочлен N(x), укажите частное и остаток (1—6): Задание 1. М(х) = х3 - Зх2 + 5х - 6, N(x) = х -- 2 Ответ: х3 - Зх2 + 5х - 6 = (х2 - х + 3) (х - 2) Задание 2. М(х) = х3- х2- 8х + 12, N(x) = x2 + 1 Ответ: х3 - х2 - 8х + 12 = (х - 1) (х2 + 1) - 9х + 13 Задание 3. М(х) = х3 - Зх + 2х - 1, N(x) = х2 + х Ответ: х3 - Зх2+ 2х - 1 = (х - 4) (х2 + х) + 6х - 1 Задание 4. М(х) = х4 + х2 + 1, N(х) = х2 + х + 1 Ответ: х4 + х2 + 1 = (х2 - х + 1) (х2 + х + 1) Задание 5. М(х) = х4 + 4, N(х) = х2 - 2х + 2 Ответ: х4 + 4 = (х2 + 2х + 2) (х2 -2х + 2) Задание 6. М(х) = х10 +х2 + 1, N(x) = x2 + x+1 Ответ: X10 + X2 + 1 = (X8 - Х7 + Х5 - X4 + Х2- X + 1) (X2 + X + 1)
Найдите остатки от деления многочлена М(х) на х; х - 1; х + 3; 2х - 4 (7—12): Задание 7. М(х) = х2 +2х - 3 Ответ: -3;0;0; 2,5 Задание 8. М(х) = х3 - 2х - 3х Ответ: 0;-4;-36; 3 Задание 9. М(х) = х4 - 7х2 - 6x + 1 Ответ: 1;-11; 163;-6,5 Задание 10. М(х) = х4 + 81 Ответ: 81; 82; 0; 48,5. Задание 11. М(х) = х6 - x5 - 6х4 - x2 + х + 6 Ответ: 6; 0; 492;-30 Задание 12. М(х) = х5 + Зx4 + Зх3 + 9х2 - 4х - 12 Ответ: -12; 0; 0; 60 Задание 13. При каком а остаток от деления многочлена М(х) -- 2х3 - Зх2 + ах - 6 на х - 2 равен 6? Решение: По теореме Везу остаток от деления М(х) на (х — 2) равен М(2). Отсюда М(2) = 2а - 2 = 6. Ответ: а = 4 Задание 14. При каком а остаток от деления многочлена М(х) = = 2х5 - Зх3 + 11х2 - х + а на х + 2 равен 3? Ответ: а = -3 Задание 15. Найдите числа а и b, если остаток от деления М(х) = 2х3 - Зх2 - ах + b на (х + 1) равен 7, а от деления на (х - 1) он равен 5. Ответ: а = 3; b = 9 Задание 16. При делении многочлена Р(х) на (х - 1) в остатке получается 2, а при делении на (х - 2) в остатке получается 1. Чему равен остаток от деления Р(х) на (х - 1)(х - 2)? Решение: Запишем многочлен Р(х) в виде Р(х) = Q(x)(x - 1)(х - 2) + ах + b, где Q(x) — частное, а (ах + b) — остаток от деления Р(х) на (х - 1)(х - 2). Используя теорему Безу, получаем
откуда а = -1, b = 3. Ответ: -х + 3 Задание 17. При каких значениях а и b многочлен М(х) = ах3 + + bх2 - 37х + 14 делится на (х2 + х - 2) без остатка? Указание: х2 + х - 2 = (х - 1)(х + 2) Ответ: а = 15, b = 8 Задание 18. При каких значениях а и b многочлен М(х) = ах3 + + bх2 - 73х + 102 делится на х2 - 5х + 6 без остатка? Решение: Так как х2 - bх + 6 = (х - 2) (х - 3), то М(х) делится на (х - 2) и на (x - 3) без остатка. Используя теорему Безу, получаем
Ответ: a = 2, b = 1 Задание 19. Составьте уравнение третьей степени, имеющее корни: а) 1; 3; -2; Ответ: а) (х - 1)(x - 2)(x + 2) = х3 - x2 - 4x + 4 = 0 b) X3 - 5x2 + 7x - 3 = 0; в) x3 - 3x2 - 2x + 6 = 0 Задание 20. Найдите многочлен наименьшей степени с целыми коэффициентами, который имел бы корнем число
Ответ: Сократите дроби (21—26): Задание 21.
Решение: Покажем на этом примере способ отыскания общих множителей (общих делителей) двух многочленов, основанный на алгоритме Евклида деления с остатком. Если М(х) = Q(x) • N(x) + R(х), то остаток R(x) имеет те же общие делители, что и многочлены М(х) и N(x), но его степень строго меньше степени делителя. Затем делим делитель N(x) на R(x) и т. д. В данном случае:
(х2 - 2х + 1) = (х - 1)2. Теперь получаем
Ответ:
Задание 22.
Ответ:
Задание 23.
Ответ:
Задание 24.
Решение: Покажем способ сокращения дроби в том случае, если известно разложение одного из многочленов на множители. Легко видеть, что 2х3 - х2 + х - 2 = 2 (х3 - 1) - х(х - 1) = 2(х - 1) (х2 + х + 1) - х(х - 1) = (х - 1) (2х2 + х + 2) Используя теорему Безу, убеждаемся, что числитель не делится на (х -1). Поэтому дробь будет сократимой только в том случае, если числитель разделится без остатка на (2х2 + х + 2), так как этот многочлен далее на множители не раскладывается. Имеем 2х4 + х3 + 4х2 + х + 2 = (х2 + 1)(2х2 + х + 2) Ответ:
Задание 25.
Ответ:
Задание 26.
Ответ: Дробь несократима.
Решите следующие уравнения (27—36), предварительно подобрав один или несколько корней многочлена. Запишите разложения входящих в эти уравнения многочленов на множители: Задание 27. X3 - 8х2 + 13х - 6 = 0 Решение: Попытаемся найти целочисленные решения этого уравнения. Все такие решения являются делителями свободного члена, т. е. числа 6. Это числа — ±1; +2; ±3; ±6. Находим, что х = 1 - корень этого уравнения. Разделив многочлен х3 - 8х2 + 13х - 6 на (х - 1), получим х3 - 8х2 + 13х - 6 = (х2 -7х + 6)(х-1) = 0 Решив квадратное уравнение х2 - 7х + 6 = 0, находим остальные решения исходного уравнения. Ответ: {1; 1; 6} Задание 28. х3 - 4х2 + х + 6 = 0 Ответ: {-1; 2; 3}; х3 - 4х2 + х + 6 = (х + 1)(х - 2)(х - 3) Задание 29. x4 - Зх3 - 8х2 + 12x- + 16 = 0 Ответ: {-1; ±2; 4}; х4 - Зх3 - 8х2 + 12х + 16 = (х + 1)(х + 2)(х - 2)(х - 4) Задание 30. x4 - Зх3 + х2 + Зх - 2 = 0 Ответ: Задание 31. x4 - 2x3 + 5х2 - 8х + 4 = 0 Ответ: (1; 1}; х4 - 2х3 + 5х2 - 8х + 4 = (х - 1)2 (х2 + 4) Задание 32. х4 - 8х3 + 48х2 - 128х + 87 = 0 Ответ: {1; 3}; х4 - 8х3 + 48х2 - 128х; + 87 = (х - 1)(х - 3)(х2 - 4х + 29) Задание 33. Зх3 - 4x2 + 5х - 18 = 0 Ответ: {2}; Зх3 - 4х2 + bх - 18 = (х - 2)(3х2 + 2х + 9) Задание 34. 27x3 + 9x2 - 48x + 20 = 0 Решение: Сделаем замену переменой, полагая t = Зх. Получим уравнение t3 + t2 - 16t + 20 = 0, у которого будем искать целочисленные решения. Ими могут быть только числа: ±1; ±2; +4; ±5; ±10; ±20. Подбираем корень t = 2. Разделив многочлен t3 + t2 - 16 + 20 на (t - 2), получим t3 + t2 - 16 + 20 = (t - 2)(t2 +3t - 10) = (t - 2)2(t + 5). Таким образом, t1 = t2 = 2; t3 = -5, откуда
Ответ:
Задание 35. Зx4 + 5x3 - 5х2 - 5х + 2 = 0 Ответ:
Задание 36. (х + 1)3 + (2х - З)3 = 27х3 - 8 Указание: Разложите правую и левую части уравнения на множители. Ответ:
Примечание. Другие уравнения высших порядков, сводящиеся к квадратным с помощью замены переменной, будут рассмотрены ниже. Решите следующие линейные системы (37—46). Для систем 37—40 приведите графическую иллюстрацию, построив соответствующие этим уравнениям прямые. Задание 37.
Ответ: (4; -2) Задание 38.
Ответ: (4; 1) Задание 39.
Ответ: (с; 2 - Зс), где с € R. Задание 40.
Ответ:
Решение: Данную систему можно легко решить подстановкой, выразив какое-либо неизвестное, например х, из первого уравнения и подставив это выражение в два других уравнения. Однако на этом примере мы приведем общий метод решения систем линейных уравнений, называемый методом Гаусса. Этот метод основан на том, что система перейдет в равносильную, если любое уравнение системы заменить суммой этого уравнения и любого другого уравнения системы, умноженного на любое число. Равносильность системы не нарушается и при перестановке местами любых двух уравнений. Заменив второе уравнение системы его суммой с первым уравнением, умноженным на ( -1), а третье уравнение — его суммой с первым, умноженным на ( -2), получим следующую, равносильную исходной, систему уравнений:
Затем заменили третье уравнение его суммой со вторым уравнением, умноженным на ( -1). Последняя из выписанных систем — система треугольного вида, равносильна исходной, но легко решается. Получаем: z = 2, из второго уравнения следует, что у = 0, а тогда из первого — что х = 1. Ответ: (1; 0; 2) Задание 42.
Ответ: (1; 1; 0) Задание 43.
Ответ: (1; 2; 1) Задание 44.
Решение: Снова применим метод Гаусса. Получаем системы:
Получаем: х = 5 - 2с; у = 2с - 4; z = с, т. е. система имеет бесконечно много решений, но все они выражаются указанным образом. Ответ: (5 - 2с; 2с - 4; с), с € R Задание 45.
Ответ: (2с - 1; с + 1; с), с € R Задание 46.
Ответ:
Задание 47. Найдите, при каких а совместна система:
Решение б): Система несовместна только в том случае, если
откуда а = -2. Геометрически указанное условие означает, что прямые, являющиеся графиками уравнений системы, параллельны, но не совпадают. При всех других значениях а система совместна. Ответ: а) а € R \ { -1} b) a € R \ {-2} Задание 48. При каких b не имеет решений система:
Решение б). Если
то система совместна (в этом случае прямые, являющиеся графиками уравнений системы, не параллельны). Следовательно, система может оказаться несовместной только при
или
Подставляя эти значения в систему,получаем:
Ответ: а) b = -3 b) Задание 49. Найдите все а, при которых решения системы
Решение: Решив данную систему, находим х = 5а - 140, у = 60 - 2а. Теперь из системы 5а - 140 > 0, 60 - 2а > 0, получаем, что 28 < а < 30. Ответ: а € (28; 30) Задание 50. Найдите все а, при которых решения системы
Ответ: Задание 51. Найдите а и b, при которых система уравнений
Ответ: а = 1, b = -1 или а = -1, b = 1 Задание 52. Числа а, b и с таковы, что система
Ответ: а = 0, b = 0, с = 2,25 или а = 2, b = -1, с = 1 Задание 53. Найдите многочлен третьей степени, который при делении на х дает в остатке 1, при делении на (х - 2) — в остатке 3, а на (х2 - 1) делится без остатка. Решение: Искомый многочлен имеет вид Р(х) = (ах + b)(х2 - 1). Используя теорему Везу, получаем
Ответ: х3 - х2 - х + 1 Задание 54. Найдите все целые числа а и b, для которых один из корней уравнения Зх3 + ах2 + bх + 12 = 0 равен
Решение: Подставим число
в уравнение и сгруппируем члены с множителем
Получим Так как а и b — целые числа, то это возможно только в том случае, если
(-12; 6)
• В отличие от систем линейных уравнений общего метода решения нелинейных систем не существует. Можно указать лишь те или иные приемы решения некоторых классов таких систем. Наиболее просто дело обстоит в том случае, если одно или несколько уравнений данной системы являются линейными. В этом случае выражаем часть переменных через другие и выполняем их подстановку в оставшиеся уравнения. Решите системы (55—66): Задание 55.
Ответ: {(5; 3)} Задание 56.
Ответ: {(4; 5); (5; 4)} Задание 57.
Ответ: {(3; 2); (2; 3)} Задание 58.
Решение: Подставляя у = 5 - х в первое уравнение, получаем квадратное уравнение х2 - 7х +6 = 0. Отсюда х1 = 1; у1 = 4; х2 = 6; у2 = -1. Ответ: {(1; 4)}; (6;-1)}
Ответ: {(5; 1)} Задание 60.
Решение: Преобразуя левую часть первого уравнения системы, получим
Ответ:
Задание 61.
Решение: Разложим левую часть второго уравнения на множители: х3 + у3 = (х + у)(х2 - ху + у2). Далее, учитывая, что х + у - 5, приходим к системе
Ответ: {(2; 3); (3; 2)} Задание 62.
Ответ: {(2; 1);(-1;-2)} Задание 63.
Указание: Можно воспользоваться формулой возведения в четвертую степень: (а + b)4 = а4 + 4а3b + 6а2b2 + 4ab3 + b4. Ответ: {(3; 2); (-2; -3)} Задание 64.
Решение: Здесь можно использовать подстановку х = 6 - у. Мы приведем другой способ. Второе уравнение разложим на множители: х4 + ху2 - 2х2 = (у2 + 2х)(у2 - х) Поэтому исходная система равносильна совокупности систем:
Ответ: {(9; -3); (4, 2)} Задание 65.
Указание: Подставьте выражения
во второе уравнение. Ответ: {(12; 6; 4); (-12; -6; -4)} Задание 66.
Решение: Умножив первое уравнение на 2 и сложив со вторым, имеем z = 5x - 11, а тогда у = 2х - 3. Подставим эти выражения в третье уравнение и получим квадратное уравнение для вычисления переменной х:
Ответ:
• Система называется симметричной относительно переменных х и у, если она не меняется при замене х на у, аунах. Симметричная система упрощается, если сделать подстановку u = х + у; v = ху. Решите симметричные системы (67—80): Задание 67.
Решение: Системы 67—80 — симметричные. Если это система двух уравнений с двумя переменными, то рекомендуется сделать замену, полагая u = х + у, v = ху и используя равенство x2 + у2 = (х + у)2 -- 2ху = u2 - 2v Для данной системы имеем
а тогда
Теперь решаем системы:
Первая система имеет решения {(1; 2); (2; 1)}, а вторая решений не имеет. Ответ: {(1; 2); (2; 1)} Задание 68.
Ответ: {(1; 2); (2; 1)} Задание 69.
Ответ: {(6; 9); (9; 6)} Задание 70.
Ответ: Задание 71.
Решение: Воспользуемся тем, что х3 + у3 =(х + у)3 - 3(х + у)ху. Сделав замену х + у = u, ху = v, получим X3 + у3 = u3 - Зuv, а исходная система примет вид
Ответ: {(4; 1); (1; 4)} Задание 72.
Указание: Положите х + у = и, ху = и и используйте равенство х3 + у3 = u3 - Зuv. Ответ: {(3; -2); (-2; 3)} Задание 73.
Ответ: {(1,2); (2, 1)} Задание 74.
Решение: Так как система симметричная, то получаем х + у = u, ху = V. Теперь используем равенство х4 + у4 - (х2 + у2)2 - 2х2у2 = [(х + у)2 - 2ху]2 - 2х2у2 = (u2 - 2v)2 - 2v2. Исходная система примет вид
2t2 + 97t - 6084 = 0, откуда t1 = 36; t2 = -134,5 (постороннее решение). Теперь находим v1 = 6; v2 = -6, откуда u2 = 25 (при v = 6); u2 = -25 (при v = -6). Следовательно, исходная система равносильна совокупности систем
{(3; 2)}, (2; 3), (-3; -2), (-2; -3)} Задание 75.
Ответ: {(3; 2), (2; 3), (-3; -2), (-2; -3)} Задание 76.
Ответ: {(3; 1), (1; 3), (-3; -1), (-1; -3)} Задание 77.
Решение: Система симметрична относительно всех переменных х, у, z. Выполним замену х + у + z = u; ху + xz + уz = v; хуz = w используя при этом равенство х3 + у3 + z3 = u3 - Зuv + Зw. Тогда данная система примет вид
в первое уравнение, получим s3 - 2s2 - 3s = 0, откуда s1 = 0; t1 = -4; s2 = 3; t2 = 2; s3 = -1; t3 = -2. Теперь решаем системы
{(2; -2; 1); (-2; 2; 1); (2, 1, -2); (1, 2; -2); (-2; 1; 2); (1; -2; 2)} Задание 78.
Указание: Учитывая, что система симметрична относительно х и у, сделайте замену х + у = u, ху = v. Ответ: {(1; -1; -2); (1; 2; 1); (-1; 1; -2); (-1; 2; -1); (2; 1; 1); (2; -1; -1)} Задание 79.
Решение: Система симметрична относительно переменных х и г. Сделав замену х + z = u, xz = v и не меняя у, получим
{(1; 3; 9); (9; 3; 1)} Задание 80.
Ответ:
Решите системы 81—85, воспользовавшись однородностью левых частей уравнений этих систем: Задание 81.
Решение: Заметим, что у = 0 не является решением системы ни при каком значении х. Поэтому система равносильна следующей:
Ответ:
Задание 82.
Ответ:
Задание 83.
Решение: Умножив первое уравнение на 3, второе на 28 и сложив результаты, получим равносильную систему
откуда подстановкой находим решения данной системы. Ответ:
Задание 84.
Ответ:
Задание 85.
Ответ:
Решите уравнения и системы, сделав подходящие замены переменных (86—93): Задание 86.
Указание: Сделайте замену х2 - 2х - 3 = t. Ответ:
Задание 87.
Указание: Сделайте замену х3 - х2 = t. Ответ: {-1; 2} Задание 88. х(х - 1)(х + 1)(х + 2) = 24 Решение: Заметим, что (х - 1)(х + 2) = х2 + х - 2. Тогда, полагая t = х2 + х, получим уравнение t2 - 2t - 24 = 0, откуда t1 = -4, t2 = 6. Уравнение х2 + х = -4 решений не имеет, а х2 + х - 6 = 0 дает x1 = -3; х2 = 2. Ответ: {-3; 2} Задание 89. (х - 4)(х - 5)(x - 6)(x - 7) = 1680 Указание: Сделайте замену t = х2 - 11х. Ответ: {-1; 12} Задание 90. (х2 + х + 1)(2x2 + 2х + 3) = 3(1 - х - х2) Ответ: {-1;0} Задание 91.
Решение: Переписав уравнение в виде
и получим t2
- 9t - 22 = 0. Отсюда t1 = -2; t2 = 11.
Первое из них не имеет решений, а второе дает
Ответ:
Задание 92.
Указание: Сделайте замену
Ответ:
Задание 93. (Зх2 - 7х- 2)2 + 5х2(3х2 - 7х - 2) = 24x4 Решение: Перепишем уравнение в виде t2 + 5x2t - 24х4 = 0, где t = Зх2 - 7х - 2, и решим его относительно переменной t. Получим t1 = -8x2; t2 = Зх2. Теперь решаем квадратные уравнения: Зх2 - 7х - 2 = -8х2, т. е. 11х2 - 7х - 2 = 0; Зх2 - 7х - 2 = Зх2, т. е. 7х + 2 = 0. Ответ:
Решите биквадратные или сводящиеся к биквадратным уравнения (94—99): Задание 94. x4 - 19x2 + 9 = 0 Ответ: {±3} Задание 95. 4x4 - Зх2 - 1 = 0 Ответ: {+1} Задание 96. х8 - 17х4+ 16 = 0 Указание: Сделайте замену t = x4. Ответ: {±2; ±1} Задание 97. 36х8 - 13х4 +1 = 0 Ответ:
Задание 98. (х - 5)4 + (х - З)4 = 2 Решение: Положим t = х - 4. Тогда исходное уравнение примет вид (t - 1)4 + (t + 1)4 = 2, т. е. 2t4 + 12t2 = 0, t = 0. Следовательно, решением исходного уравнения является только х = 4. Ответ: {4} Задание 99. (х + З)4 + (х - 1)4 = 82 Указание: Сделайте замену t = х + 1. Ответ: {-2; 0} Решите возвратные уравнения 100—103 (см. указания и решения к этим задачам): Задание 100. х4 + 5х3
+ 2х2 + 5х + 1 = 0 Уравнение является возвратным. Записав его в виде
уравнение t2 + 5t = 0, откуда t1 = 0; t2 = -5. Теперь решаем уравнения
Первое не имеет решений, а второе дает корни
Ответ:
Задание 101. 4х4 - 8х3 + Зх2 - 8х + 4 = 0 Указание: Разделите обе части уравнения на х2 и сделайте замену
Ответ:
Задание 102. х5 + 2х4 + 2х3 + 2х2 + х = 0 Ответ: {-1; 0} Задание 103. 2х4 + Зх3 - 4х2 - 3х + 2 = 0 Указание: Поделите обе части уравнения на х2 и сделайте замену, положив
Ответ:
Решите уравнения и системы уравнений (104—120): Задание 104. (х - З)4 + (х - 2)4 = (2х - 5)4 Решение: Положим u = х - 3; v = х - 2. Тогда исходное уравнение примет вид u4 + v4 = (u +v)4, т. е. 2uv(2u2 + 3uv + 2u2) = 0. Отсюда: либо u = 0, а тогда х = 3, либо v = 0, а тогда x = 2, либо 2u2 + + Зuv + 2v2 = 0. Но последнее уравнение ненулевых решений не имеет. Ответ: {2, 3} Задание 105. (2х + 1)4 + (Зх - 1)4 = 625х4 Указание: Положите u = 2х + 1; v = Зх - 1 и запишите уравнение в видеu4 + v4 = (u + v)4. Далее см. решение задачи 104. Ответ:
Задание 106. (7х + З)4 + (2х - б)4 = (Зх + 7)4 + (6х - 2)4 Решение: Запишем уравнение в виде (7х + З)4 - (Зх + 7)4 = (6х - 2)4 - (2х - 6)4 и разложим обе части равенства на множители. Получим (10х + 10)(4х - 4) [(7х + З)2 + (Зх + 7)2] = (8х - 8)(4х + 4) [(6х - 2)2 + (2х - 6)2], откуда x1 = 1, х2 = -1, а остальные корни найдем, решив уравнение 5[(7х + З)2 + (Зх 4 7)2] = 4[(6х - 2)2 + (2х - б)2]. Подсчет показывает,
Задание 107. |11 + х + у -4ху| + |х2у + ху2 - 20| = 0 Указание: где u = ху; v = х + у. Ответ:
Задание 108. |2ху + у2 - 4x - Зу + 2| + |ху + Зу2 - 2x - 14у + 16| = 0 Решение: Уравнение равносильно системе
5у2 - 25у + 30 = 0, откуда у = 2 или у = 3. Теперь решаем системы уравнений
Ответ: {(-1; 3); (с; 2)}; с € R Задание 109.
Ответ:
Задание 110.
Ответ:
Задание 111.
Указание: Положите х2у3 = u; х3у2 = v. Ответ: {(1; 2)} Задание 112.
Указание: Запишите систему в виде
Ответ:
Задание 113.
Указание: Воспользуйтесь тем, что система симметричная и сделайте замену х + у - u; ху = V. Ответ: {(1; 2); (2; 1)} Задание 114.
Ответ:
Задание 115.
Указание: Воспользуйтесь однородностью первого уравнения. Ответ: {(0; 0); (3; 2); ( -2; -3)} Задание 116.
Решение: Система симметрична относительно переменных х и у. Сделаем замену u = х + у; v = ху, учитывая, что х2 + у2
= u2 - 2v Получим u = Зz; Подставляя в третье уравнение выражения u = Зz, u2 - 2v = 5z, имеем Зz(5z - v) = 9z. Отсюда либо z = 0, а тогда и х = у = 0, либо v = 5z - 3. Теперь из второго уравнения
получаем 9z2 - 2(5z - 3) = 5z,
Таким образом, приходим к системам
из которых находим все решения исходной системы. Ответ: ((0; 0; 0); (2; 3; 1); (3; 2; 1);
Задание 117.
Ответ:
Задание 118.
Указание: Выразите у и z через х из первых двух уравнений и подставьте в третье. Ответ: {(1; 0; 3); (-1; -2; 1)} Задание 119.
Решение: Первое уравнение системы является квадратным относительно (Зх - 2у) = t. Действительно, 9х2 - 12ху + 4(у2 = (Зх - 2у)2 = t2, 6х - 4у = 2t. Таким образом, t2 + 2t + 1 = 0 <=>t = -1и система принимает вид
Ответ:
Задание 120.
Ответ: Задание 121. При всех а и b решите системы уравнений:
Решение а): Прибавив к первому уравнению второе, умноженное на 3, получим
0 • х всегда равно нулю и, следовательно, система не имеет решений. Если 2а + 3 = b + 3 = 0,
то первое уравнение системы выполняется при всех х, т. е. решениями системы
служат любые числа х и у, связанные равенством х + у = 1. при
при
Задание 122. При всех а решите систему уравнений
Ответ: при
при
Задание 123. В зависимости от а найдите число решений системы
Ответ: При
нет решений; при
восемь решений. Задание 124. При каких а система уравнений
имеет единственное решение? Указание: Если данное уравнение имеет единственное решение, то в этом решении значение х равно нулю (так как если пара
— решение системы, то
— тоже решение). Подставив х = 0 в систему, найдите два значения параметра а, при которых возможна единственность. Подстановкой этих значений параметра в исходную систему одно из значений можно будет отбросить. Ответ: а = 2 Задание 125. При каких а система уравнений
Указание: Решив первое уравнение системы, найдите множество его решений [1; 6] U {-3; -2}. Второе уравнение имеет решения х1 = а - 4 и Х2 = а. Теперь выберите значения а, при которых X1 и х2 принадлежат множеству [1; 6] U {-3; -2}. Ответ:
Задание 126. Найдите все значения параметра а, при которых система
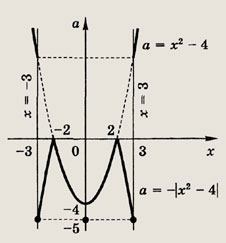
Ответ: а = +1 Задание 127. Сколько различных решений в зависимости от а имеет уравнение |х4 - 13х2 + 36| = а(х2 - 9)? Решение: Разложив выражение под знаком модуля на множители, перепишем исходное уравнение в виде |(х2 - 9)(x2 - 4)| = а(х2 - 9)<=> |х2 - 9||х2 - 4| = а(х2 - 9). Рассмотрим три случая: 1) если х2 - 9 = 0 т. е. х = ±3, то уравнение верно при всех а; 2) если х2 - 9 > 0, то уравнение имеет вид a = |х2 - 4|; 3) если х2 - 9 < 0 (-3 < х < 3), то a = - |x2 - 4|. Изобразим множество этих точек на плоскости хОа.
Количество решений уравнения — это количество точек пересечения горизонтальной прямой с построенным мно жеством. Ответ: при
два решения; при
четыре решения; при а = -4 => пять решений; при а € (-4; 0) => шесть решений. Задание 128. Решите уравнение
Ответ
при
при
при
Поделитесь этой записью или добавьте в закладки |
Полезные публикации |
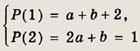
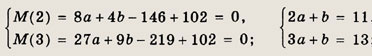
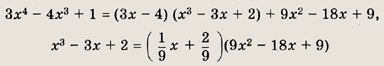
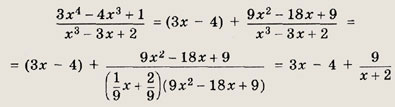
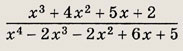
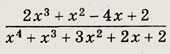
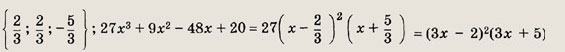
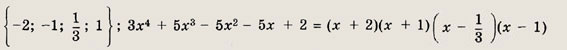

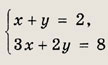
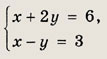
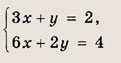
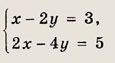
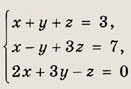
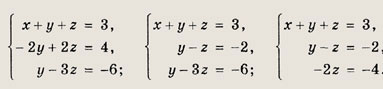
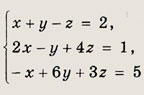
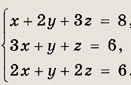
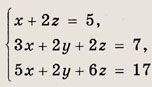
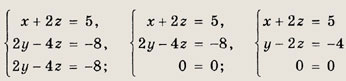
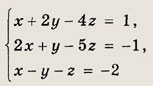
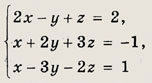

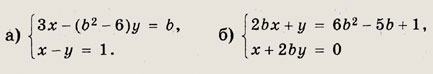
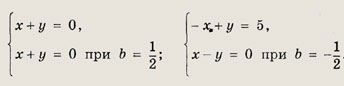
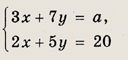
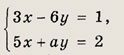
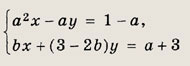
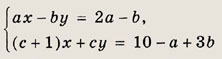
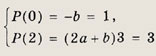

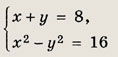
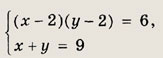
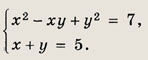
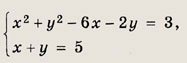
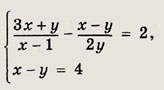
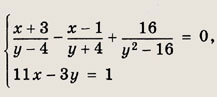
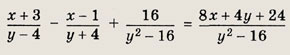
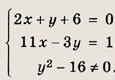
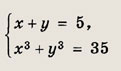
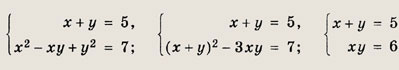
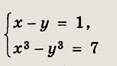
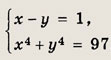

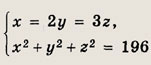
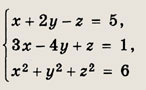
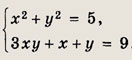

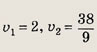
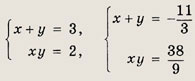
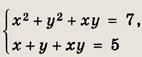
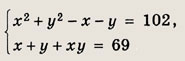
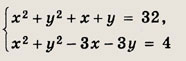
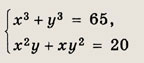
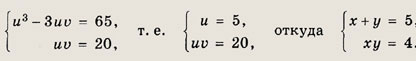
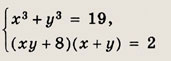
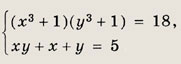
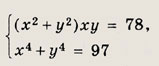
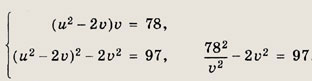
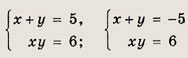
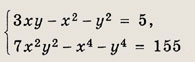
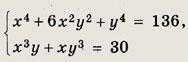
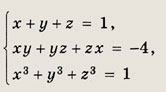

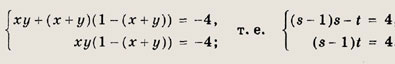
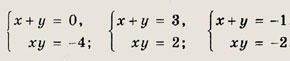
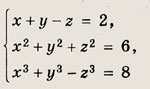
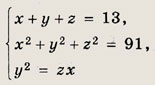
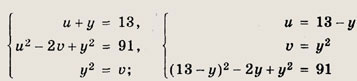
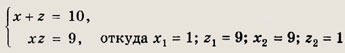
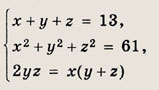
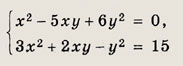
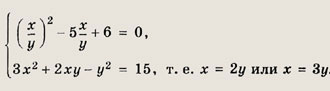
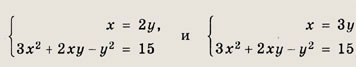
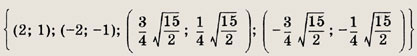
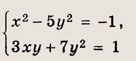
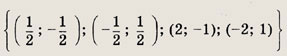
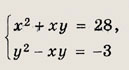
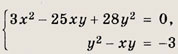
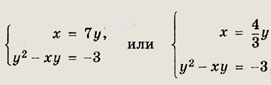
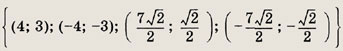
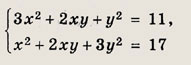
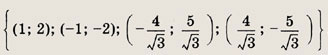
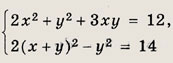
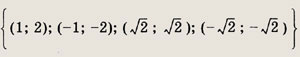
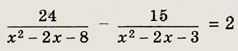
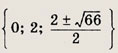
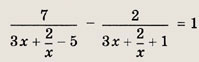
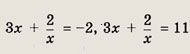
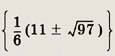
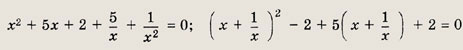
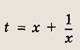
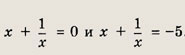
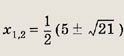
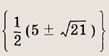
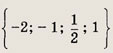
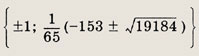

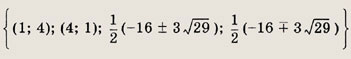
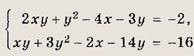
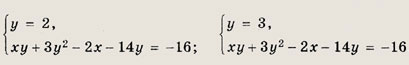
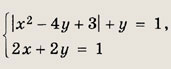
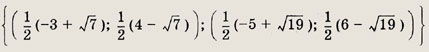
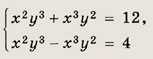
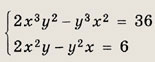
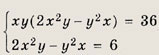
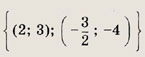
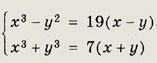
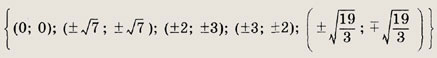
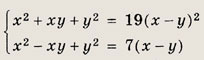
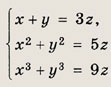
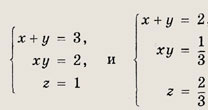
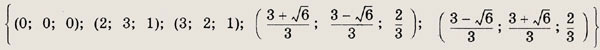
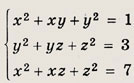
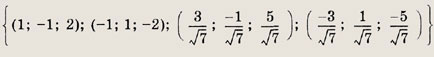
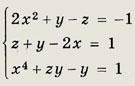
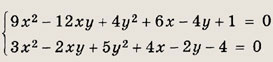
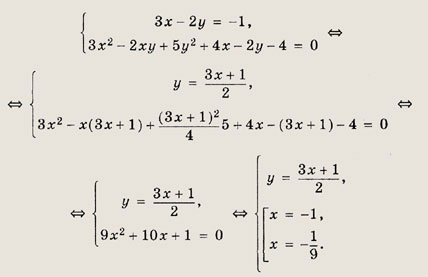
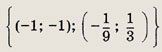
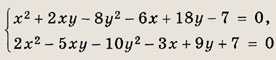

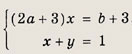
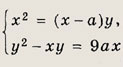
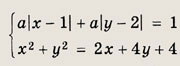
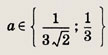
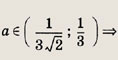
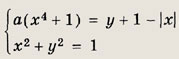
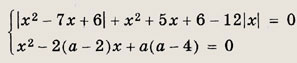
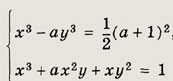
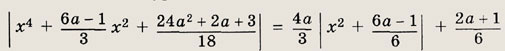
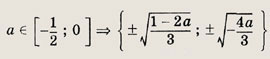
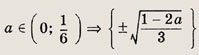
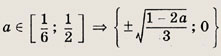
 Главная
Главная