
Формирование инвестиционного портфеля
| Категория реферата: Рефераты по информатике, программированию
| Теги реферата: bestreferat ru, реферат катастрофы
| Добавил(а) на сайт: Альбертина.
Предыдущая страница реферата | 13 14 15 16 17 18 19 20 21 22 23 | Следующая страница реферата
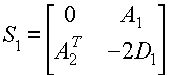
![]()
Можно показать, что
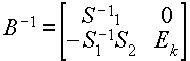
Видно, что зная матрицу S1-1 можно легко получить значение матрицы B-1 . Используя общий вид переходов, а также их общее свойство, сводящееся к замене одного вектора на другой, можно применить для нахождения S1-1 известную формулу Фробениуса, и получить рекуррентные формулы, связывающие матрицы S1-1 на соседних итерациях. Это позволяет избежать непосредственного обращения матрицы на каждом шаге алгоритма, прибегая к нему через определенный промежуток времени с целью коррекции накопившейся ошибки вычисления.
4. Задача квадратичного программирования с параметром в правых частях ограничений.
4.1 Постановка задачи
Задачей параметрического квадратичного программирования с параметром в правых частях ограничений будем называть следующую задачу выпуклого программирования:
|
|
(4.1.1) |
Требуется найти вектор-функцию x*(m ) , минимизирующую целевую функцию при каждом m . Интервал изменения параметра может быть и неограниченным.
4.2 Некоторые свойства решения параметрической задачи квадратичного программирования.
Пусть получено решение задачи (4.1.1) при некотором значении параметра, равном m 0 . Это означает, что получен вектор x*(m 0) , а также набор индексов Á (m 0) , и порожденный им оптимальный базис. Рассмотрим множество таких m , для которых это решение остается оптимальным и допустимым. Для этого запишем условия Куна-Таккера:
|
|
(4.1.2) |
Как следует из постановки задачи, правую часть выражения (4.1.2) можно представить в следующем виде:
Рекомендуем скачать другие рефераты по теме: реферат предприятие, реферат по русскому.
Категории:
Предыдущая страница реферата | 13 14 15 16 17 18 19 20 21 22 23 | Следующая страница реферата
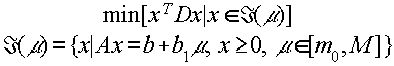
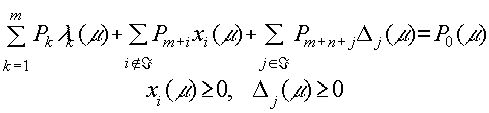
 Главная
Главная