Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

На рис. 13.43 показано также контекстно-зависимое меню, которое появляется при нажатии правой клавиши мыши в момент, когда курсор ее находится в поле выделенного графика. Нетрудно заметить, что с помощью этого меню (и открываемых им подменю) можно получить доступ к опциям трехмерной графики и выполнить необходимые операции форматирования, такие, как включение цветовой окраски, выбор ориентации фигуры и т.д.

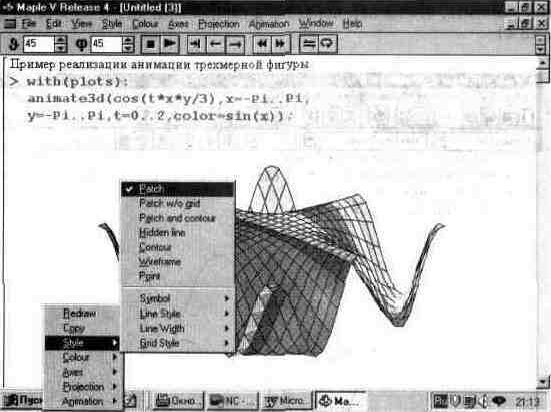
Рис. 13.43. Подготовка анимационного ЗО-графика.

13.6.12. Использование для анимации опции insequence

Еще один путь создания анимационных рисунков — создание ряда графических объектов р1, р2, рЗ и т.д. и их последовательный вывод с помощью функции:

display(pl,p2,p3,...,insequence=true) display3d(pl,p2,p3...,insequence=true)

Здесь основным моментом является применение опции insequence=true. Именно она обеспечивает вывод одного за другим серии графических объектов р1, р2, рЗ и т.д.

13.7. Графика пакета plottools 13.7.1. Состав пакета plottools

Инструментальный пакет графики plottools служит для создания графических примитивов, строящих элементарные геометрические объекты на плоскости и в пространстве: отрезки прямых и дуг, окружности, конусы, кубики и т.д. Его применение позволяет разнообразить графические построения и строить множество графиков специального назначения. В пакет входят следующие графические примитивы:

arc arrow circle cone cuboid curve cutin cutout cylinder disk dodecahedron ellipse ellipticArc hemisphere hexahedron hyperbola icosahedron line octahedron pieslice point polygon rectangle semitorus sphere tetrahedron torus

Вызов примитивов пакета осуществляется после загрузки пакета в память ПК командой with(plottools). Обычно примитивы используются для задания графических объектов, которые затем выводятся функцией display. Возможно, применение этих примитивов совместно с различными графиками.

13.7.2. Примеры применения примитивов пакета plottools

Большинство примитивов пакета plottools имеет довольно очевидный синтаксис. Например, для задания дуги используется примитив

агс(с, г, а..Ь, ...),

где с — список с координатами центра окружности, к которой принадлежит дуга, г — радиус этой окружности, а..Ь — диапазон углов. На месте многоточия могут стоять обычные опции, задающие цвет дуги, толщину ее линии и т.д. Все формы записи графических примитивов и их синтаксис можно найти в справочной системе.

На рис. 13.44 показано применение нескольких примитивов двумерной графики для построения дуги, окружности, закрашенного красным цветом эллипса и отрезка прямой. Кроме того, на графике показано построение синусоиды. Во избежание искажений пропорций фигур надо согласовывать диапазон изменения переменной х.

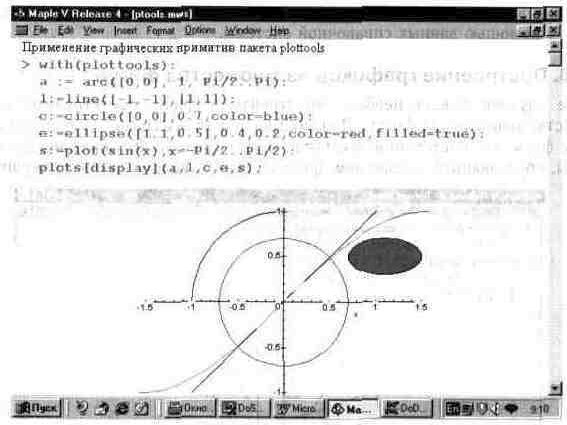
Рис. 13.44. Примеры применения примитивов 20-графики пакета plottools.

Аналогичным образом используются примитивы построения трехмерных фигур. На рис. 13.45 показано совместное построение двух пересекающихся кубов и сферы в пространстве. Нетрудно заметить, что графика пакета приблизительно (с точностью до сегмента фигур) вычисляет области пересечения фигур. С помощью контекстно-зависимого меню правой клавиши мыши (рис. 13.45) можно устанавливать условия обзора фигур, учитывать перспективу при построении и т.д. В частности, фигуры на рис. 13.45 показаны в перспективе.

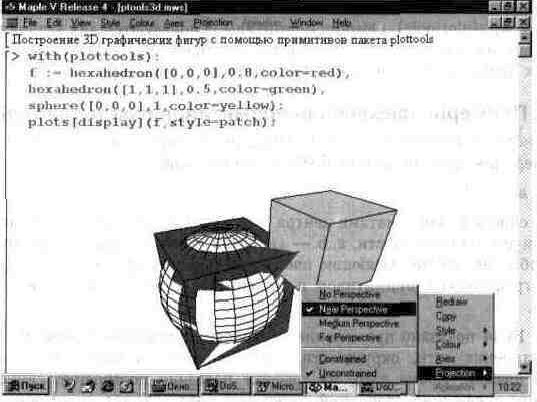
Рис. 13.45. Примеры применения примитивов 30-графики пакета plottools.

С другими возможностями этого пакета читатель теперь справится самостоятельно или с помощью данных справочной системы.

13.7.3. Построение графиков из множества фигур

В ряде случаев бывает необходимо строить графики, представляющие собой множество однотипных фигур. Для построения таких графиков полезно использовать функцию повторения seq(f,i=a..b). На рис. 13.46 показано построение фигуры, образованной вращением прямоугольника вокруг одной из вершин.

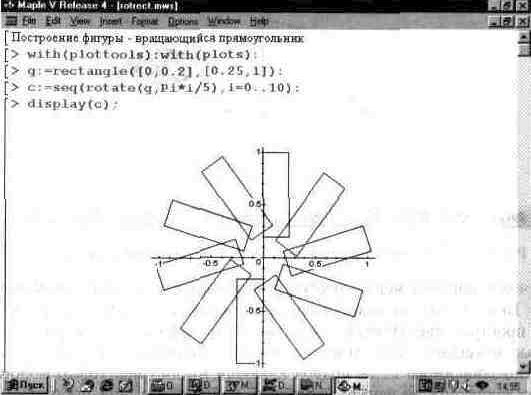
Рис. 13.46. Построение фигуры, образованной вращением прямоугольника.

В этом примере полезно обратить внимание еще и на функцию поворота фигуры — rotate. Именно сочетание этих двух функций (мультиплицирования и поворота базовой фигуры — прямоугольника) позволяет получить сложную фигуру, показанную на рис. 13.46.

13.8. Графическое представление решений дифференциальных уравнений

13.8.1. Применение функции odeplot пакета plots

Рекомендуем скачать другие рефераты по теме: евгений сочинение, шпаргалки по праву.





Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата