Предыдущая страница реферата | 14  15  16  17  18  19  20  21  22  23  24 | Следующая страница реферата

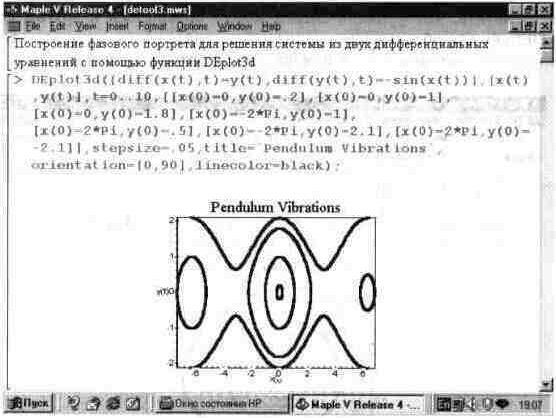
Рис. 13.52. Пример решения системы из двух дифференциальных уравнении с помощью функции DEplot3d.

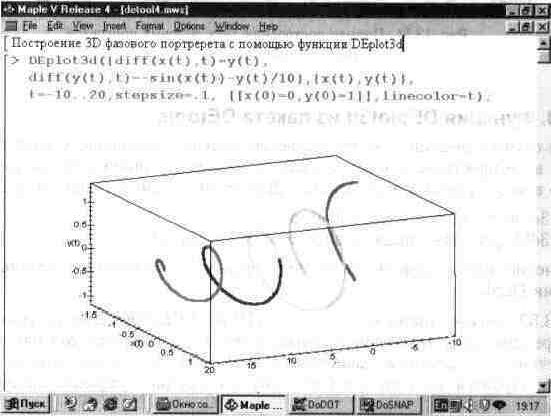
Рис. 13.53. Пример решения системы из двух дифференциальных уравнении с построением трехмерного фазового портрета.

Возможности функции DEplot позволяют решать системы дифференциальных уравнении с числом последних и больше двух — рис. 13.54, например. Однако в этом случае число решений, представляемых графически, выходит за пределы, допустимые ЗИ-графикои. При этом от пользователя зависит, какие из зависимо-

стен опускаются при построении, а какие строятся. Так, на рис. 13.54 в пространстве построены две кривые решения.

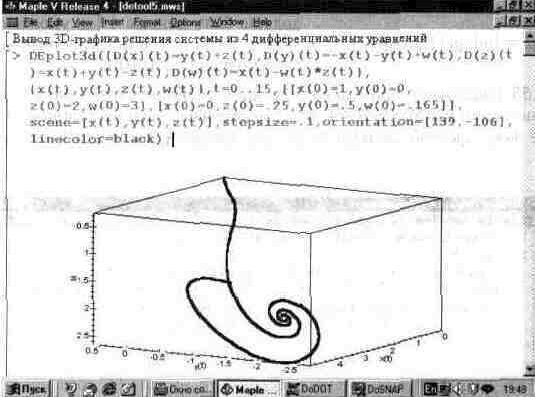
Рис. 13.54. Решение системы из четырех дифференциальных уравнении.

Нередко таким образом можно вывести на построение и иные зависимости. Однако их число обычно приходится ограничивать из-за потери наглядности графика при большом числе линий.

13.8.4. Функция PDEplot пакета DEtools

Еще одна функция пакета DEtools — DEtools[PDEplot] служит для построения графиков решения систем с квазилинейными дифференциальными уравнениями первого порядка в частных производных:

Р(х,у,и) * D[l](u)(x,y) + Q(x,y,u) * D[2](u)(x,y) = R(x,y u),

так что

P их + Q uy = R,

где P, Q и R зависят только от х, у и и(х,у), при этом dx/dt = P, dy/dt = Q, du/dt = R.

Эта функция используется в следующем виде:

PDEplot(pdiffeq, var, Lcurve, srange, о) PDEplot(pdiffeq, var, i_cLirve, srange, xrange, yrange, urange, o)

Здесь, помимо отмеченных ранее параметров, pdiffeq — квазилинейные дифференциальные уравнения первого порядка (PDE), vars — независимая переменная и Lcurve — начальные условия для параметрических кривых ЗО-поверхности. Помимо опций, указанных для функции DEplot, здесь могут использоваться следующие опции:

basechar = TRUE,FALSE,ONLY — устанавливает показ базовых характеристик кривых;

basecolour, basecolor = b_colour — устанавливает цвет базовых характеристик;

initcolour, initcolor = Lcolour — инициализация цветов;

numchar = integer — задает число отрезков кривых, которое не

должно быть меньше 4 (по умолчанию 20);

numsteps = [integerl,integer2] — задает число шагов интегрирования

(по умолчанию [10,10]).

Рис. 13.55 показывает применение функции PDEplot. Этот пример, взятый из справочной системы Maple V R4, показывает, насколько необычным может быть решение даже простой системы дифференциальных уравнений в частных производных.

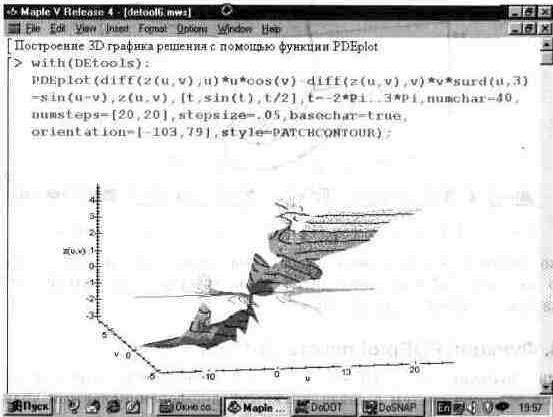
Рис. 13.55. Пример применения функции PDEplot.

В данном случае решение представлено трехмерной фигурой весьма нерегулярного вида.

Другой пример использования функции PDEplot показан на рис. 13.56. Он иллюстрирует комбинированное построение графиков решения разного типа с применением функциональной закраски, реализуемой по заданной формуле с помощью опции initcolor.

Рекомендуем скачать другие рефераты по теме: евгений сочинение, шпаргалки по праву.





Предыдущая страница реферата | 14  15  16  17  18  19  20  21  22  23  24 | Следующая страница реферата