Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата

dirgrid = [integer,integer] — число линий сетки (о умолчанию 20(20);

iterations = integer — количество итераций, представленное целым

числом;

linecolour, linecolor = line_info— цвет линии (задается 5 способами);

method='rk4' — задает метод решени 'euler', 'backeuler',

'impeuler' и 'rk4';

obsrange = TRUE,FALSE — задает (при TRUE) прерывание вычислений,

если кривая решения выходит из области обзора;

scene = [name,name] — задает имена зависимых переменных, для

которых строится график;

stepsize = h — шаг решения, по умолчанию равный

abs((b-a))/20, и представленный вещественным

значением.

На рис. 13.50 показано решение системы дифференциальных уравнений

х- (t)=x(t)*(l-y(t)) у' (t)=0,3*y(t)*(x(t)-l),

описывающих модель Лотка-Вольтерра при заданных в документе изменениях t, x(t) и y(t). Решение представлено в виде векторного поля, стрелки которого становятся касательными к кривым решения. Обратите внимание на функциональную закраску стрелок векторного поля.

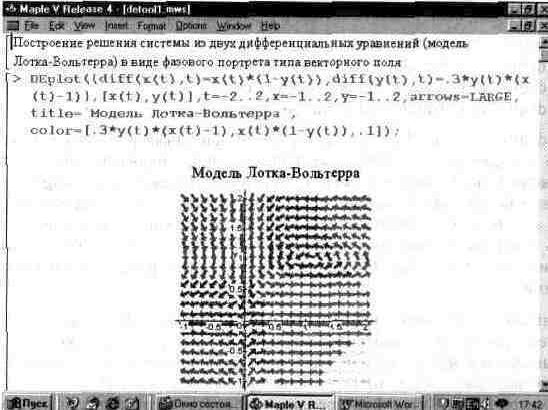
Рис. 13.50. Решение системы дифференциальных уравнении Лотка-Вольтерра с выводом в виде графика векторного поля.

Еще интересней вариант графиков, представленный на рис. 13.51. Здесь помимо векторного поля построены фазовые портреты решения с использованием функциональной закраски их линий. Фазовые портреты построены для двух наборов начальных условий: х(0)= у(0)=1.2 и х(0)=1 и у(0)=0.7.

Следует отметить, что функция DEplot может обращаться к другим функциям пакета DEtools для обеспечения специальных графических возможностей, таких как построение векторного поля или фазового портрета решения.

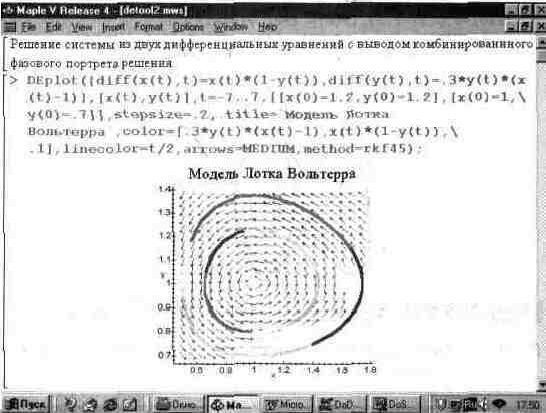
Рис. 13.51. Пример построения двух фазовых портретов на фоне векторного поля.

13.8.3. Функция DEplot3d из пакета DEtools

В ряде случаев решение систем дифференциальных уравнений удобно представлять в виде пространственных кривых — например, линий равного уровня или просто в виде кривых в пространстве. Для этого служит функция DEplot3d.

DEplot3d(deqns, vars, trange, initset, о) DEplot3d(deqns, vars, trange, yrange, xrange, initset, o)

Назначение параметров и опций этой функции аналогично указанному для функции DEplot.

Рис. 13.52 поясняет применение функции DEplot3d для решения системы из двух дифференциальных уравнений с выводом фазового портрета колебаний в виде параметрически заданной зависимости x(t), y(t). В данном случае фазовый портрет строится на плоскости по типу построения графиков линий равной высоты.

Другой пример (рис. 13.53) показывает решение системы из двух дифференциальных уравнений с построением объемного фазового портрета. В этом случае используется координатная система ЗD-гpaфики и графические построения соответствуют параметрическим зависимостям x(t), y(t) и z(t). Вид фазового портрета напоминает разворачивающуюся в пространстве объемную спираль. Функциональная окраска ее делает график эффектным, что, увы, теряется при черно-белом воспроизведении графика.

Рекомендуем скачать другие рефераты по теме: евгений сочинение, шпаргалки по праву.





Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата