Предыдущая страница реферата | 14  15  16  17  18  19  20  21  22  23  24 | Следующая страница реферата

Еще раз отметим, что, к сожалению, рисунки в данной книге не дают представления о цвете. Поэтому наглядность решений, видимых на экране дисплея, существенно выше.

13.8.5. Графическая функция dfieldplot

Графическая функция dfieldplot служит для построения векторного поля (поля направления) по результатам решения дифференциальных уравнений. Фактически эта функция как бы входит в функцию DEplot и при необходимости вызывается последней. Но она может использоваться и самостоятельно, что показывает

рис. 13.57, на котором показан пример решения следующей системы дифференциальных уравнений: x'(t)=x(t)*(l-y(t)), y'(t)=0.3*y(t)*(x(t)-l).

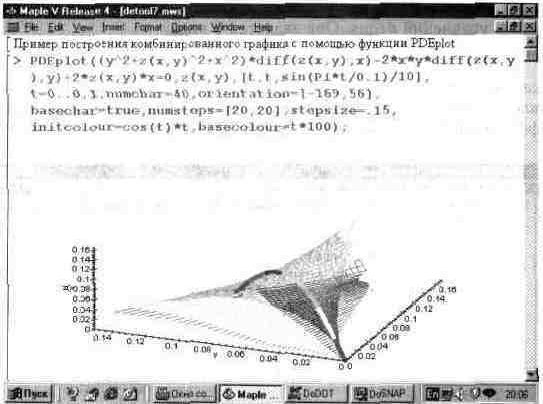
Рис. 13.56. Построение комбинированного графика с помощью функции PDEplot.

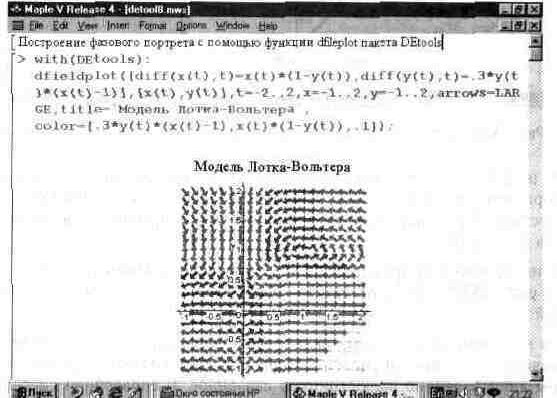
Рис. 13.57. Построение фазового портрета в виде графика векторного поля.

Обратите внимание на использование опций в этом примере, в частности на вывод надписи на рисунок на русском языке. В целом список параметров функции phaseportrait аналогичен таковому для функции DEplot (отсутствует лишь задание начальных условий).

13.8.6. Графическая функция phaseportrait

Графическая функция phaseportrait служит для построения фазовых портретов по результатам решения одного дифференциального уравнения или системы дифференциальных уравнений deqns. Она задается в виде:

phaseportrait(deqns, vars,trange,inits,o)

При задании уравнений достаточно указать их правые части. На рис. 13.58 представлен пример применения функции phaseportrait для решения системы из трех дифференциальных уравнений первого порядка.

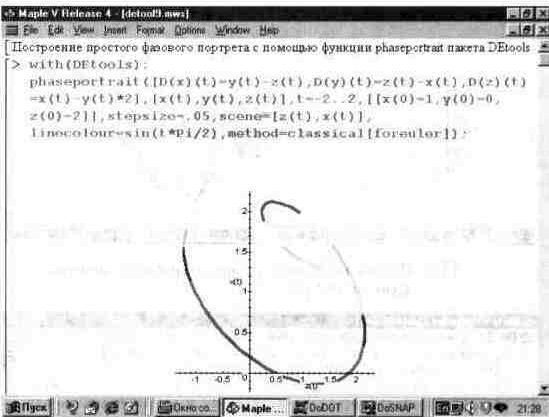
Рис. 13.58. Построение фазового портрета с помощью функции phaseportrait.

В этом примере система дифференциальных уравнений задана с применением оператора дифференцирования D. Функциональная окраска линии фазового портрета достигается использованием опции linecolor, в правой части которой задана формула для цвета.

Еще более интересный пример решения дифференциального уравнения представлен на рис. 13.59. Здесь построены фазовые портреты для асимптотических решений.

В целом надо отметить, что возможности визуализации решений дифференциальных уравнений с помощью системы Maple V весьма велики и приведенные выше примеры лишь частично иллюстрируют сказанное. В справочной системе можно найти ряд других весьма эффектных решений систем дифференциальных уравнений с визуализацией последних.

13.9. Иллюстративная графика пакета student

Пакет student имеет три графические функции для иллюстрации интегрирования методом прямоугольников:

leftbox(f(x), x=a..b, о) или leftbox(f(x), x=a..b, n, 'shading'=, o) rightbox(f(x), x=a..b, о) или rightbox(f(x), x=a..b, n, o) middlebox(f(x), x=a..b, о) или middlebox(f(x), x=a..b, n, o),

Здесь: f(x) — функция переменной х, х — переменная интегрирования, а — левая граница области интегрирования, b — правая граница области интегрирования, n — число показанных прямоугольников, color — цвет прямоугольников, о — опции (см. plot,options).

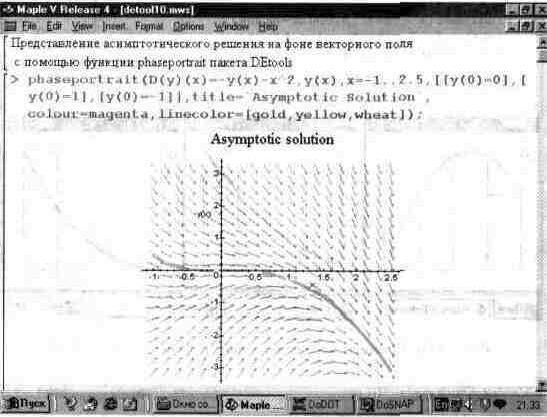
Рис. 13.59. Построение асимптотического решения на фоне графика векторного поля.

В этих функциях прямоугольники строятся соответственно слева, справа и посередине относительно узловых точек функции f(x), график которой также строится. Кроме того, имеется функция для построения касательной к заданной точке х=а для линии, представляющей f(x):

showtangent (f(x), х = а).

Рис. 13.60 показывает все эти возможности пакета student. Четыре вида графиков здесь построены в отдельных окнах.

Возможности графики пакета student ограничены. Но они дают как раз те возможности, которые отсутствуют в основных средствах графики.

13.10. Графика статистического пакета stat

Рекомендуем скачать другие рефераты по теме: евгений сочинение, шпаргалки по праву.





Предыдущая страница реферата | 14  15  16  17  18  19  20  21  22  23  24 | Следующая страница реферата