Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Причем элементы сij  и bij определяются по формулам:

,

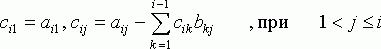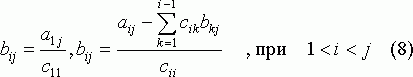
Уравнение (7) можно записать в следующем виде:

CBx=b.          (9)

Произведение Bx матрицы B на вектор-столбец x является вектором-столбцом, который обозначим через y:

Bx=y.        (10)

Тогда уравнение (9) перепишем  в виде:

Cy=b.     (11)

Здесь элементы сij известны, так как матрица А системы (7) считается уже разложенной на произведение двух треугольных матриц С и В.

Перемножив матрицы в левой части равенства (11), получаем систему уравнений из которой получаем следующие формулы для определения неизвестных:

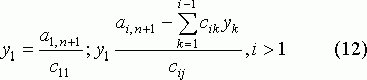
неизвестные yi удобно вычислять вместе с элементами bij.

После того как все yi определены по формулам (12), подставляем их в уравнение(10).

Так как коэффициенты bij определены (8), то значения неизвестных, начиная с последнего, вычисляем по следующим формулам:

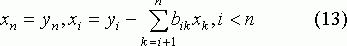
К прямым методам, использующим свойство разреженности А, можно отнести: алгоритм минимальной степени, алгоритм минимального дефицита, древовидное блочное разбиение для асимметричного разложения, методы вложенных или параллельных сечений и др.

Метод Гаусса.

Пусть дана система

Ax = b

где А – матрица размерности m x m.

В предположении, что , первое уравнение системы

,

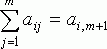делим на коэффициент , в результате получаем уравнение

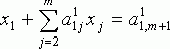
Рекомендуем скачать другие рефераты по теме: сочинение татьяна, мировая торговля.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата