Алгоритм компактного хранения и решения СЛАУ высокого порядка
| Категория реферата: Рефераты по математике
| Теги реферата: океан реферат, бесплатные банки рефератов
| Добавил(а) на сайт: Bojkov.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
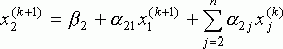
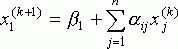
где k=0,1,...,n
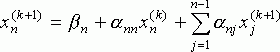
Метод Ланцоша.
Для решения СЛАУ высокого порядка (1), матрица, коэффициентов которой хранится в компактном нижеописанном виде, наиболее удобным итерационным методом является метод Ланцоша [4], схема которого имеет вид:
(18)
где
Преимуществом данного метода является его высокая скорость сходимости к
точному решению. Кроме того, доказано, что он обладает свойством «квадратичного
окончания», т.е. для положительно определенной матрицы можно гарантировано
получить точное решение при количестве итераций 
. Размер требуемой памяти
на каждой итерации не изменяется, т.к. не требует преобразование матрицы 
. В качестве критерия
остановки данного итерационного процесса обычно используют соотношение
, (19)
где 
- заданная точность. В
качестве другого критерия сходимости иногда удобнее использовать
среднеквадратичную разность между решениями, полученными на соседних итерациях:
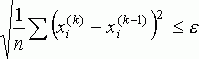(20)
Среднеквадратичную разность необходимо контролировать при выполнении каждых k наперед заданных итераций.
Отдельно следует рассмотреть проблему выбора начального приближения 
. Доказывается, что при
положительно определенной матрице 
, итерационный процесс
(18) всегда сходится при любом выборе начального приближения. При решении
контактных задач, когда для уточнения граничных условий в зоне предполагаемого
контакта требуется большое количество решений СЛАУ вида (1), в качестве
начального приближения для первого расчета используется правая часть системы
(1), а для каждого последующего пересчета - решение, полученное на предыдущем.
Такая схема позволяет значительно сократить количество итераций, необходимых
для достижения заданной точности (19) или (20) [10,11].
2 МЕТОДЫ КОМПАКТНОГО ХРАНЕНИЯ МАТРИЦЫ ЖЕСТКОСТИ
Матрица жесткости, получающаяся при применении МКЭ, обладает симметричной структурой, что позволяет в общем случае хранить только верхнюю треугольную часть матрицы. Однако для задач с большим количеством неизвестных это так же приводит к проблеме нехватки памяти. Предлагаемый в данной работе метод, позволяет хранить только ненулевые члены матрицы жесткости. Суть его заключается в следующем.
Первоначально, с целью выявления связей каждого узла с другими, производится анализ структуры дискретизации области на КЭ. Например, для КЭ - сетки, изображенной на рис. 1, соответствующая структура связей будет иметь вид:
|
№ узла |
1 |
2 |
3 |
4 |
5 |
6 Рекомендуем скачать другие рефераты по теме: сочинение татьяна, мировая торговля. Категории:Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
Главная