Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата

.

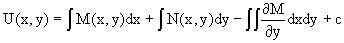Так как общее решение исходного дифференциального уравнения записывается в виде U(x,y)=c=const, то, заменяя две постоянных на одну, получаем следующий вид общего решения уравнения

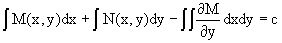или

.

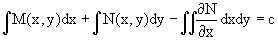Пример 1. Дано дифференциальное уравнение

(6x2y2+6xy-1)dx+(4x3y+3x2y+2y)dy=0.

В нем M(x,y)=6x2y2+6xy-1, N(x,y)=4x3y+3x2y+2y. Из 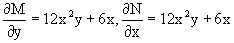и тождества ,

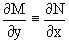Следует, что данное уравнение является уравнением в полных дифференциалах. Проведем его решение в два этапа.

На первом решаем уравнение

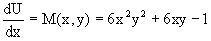или dU=(6x2y2+6xy-1)dx,

в котором переменная y считается закрепленной. Интегрируя это уравнение, получаем

U(x,y)=2x3y2+3x2y-x+h(y).

На втором этапе определяем вид функции h(y), используя для этого соотношение

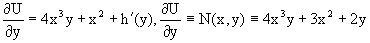
и дифференциальное уравнение для h и y

4x3y+3x2+h/(y)=4x3y+3x2+2y или .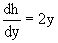

Интегрируя последнее, получаем h=y2+c. Общий интеграл исходного уравнения тогда можно записать в виде

2x3y2+3x2y-x+y2=c.

Пример 2. Найти решение уравнения

2xsinydx+(3y2+x2cosy)dy=0.

Проверяем, является ли оно уравнением в полных дифференциалах? Для этого из M(x,y)=2xsiny, N(x,y)=3y2+x2cosy

Находим

.

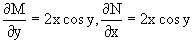Так как, очевидно, выполняется условие

,

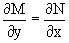Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.





Предыдущая страница реферата | 10  11  12  13  14  15  16  17  18  19  20 | Следующая страница реферата