Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата

Называемое характеристическим. Его корни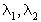, как известно, определяются формулами

.

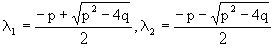Возможны следующие три случая для вида корней 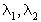этого уравнения:

1) корни уравнения – действительные и различные;

2) корни – действительные и равные;

3) корни уравнения – комплексно-сопряженные.

Для каждого из этих случаев однородное дифференциальное уравнение имеет свой вид общего интеграла.

Случай 1. Дискриминант характеристического уравнения положителен, т.е. p2-4q>0. Тогда оба корня действительные и различные. В этом случае общее решение однородного уравнения имеет вид

,

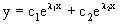где c1, c2 – произвольные постоянные.

Действительно, если 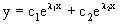, то , .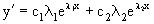

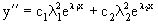Подставляя выражения для y,y/ и y// в уравнение получим

.

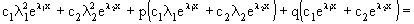
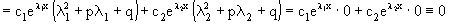Случай 2. Дискриминант характеристического квадратного уравнения равен нулю, т.е p2-4q=0.

Тогда оба корня 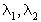действительные и равные, т.е. .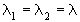

В этом случае общее решение однородного уравнения имеет вид

.

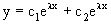Случай 3. Дискриминант характеристического квадратного уравнения отрицателен, т.е. p2-4q<0.

Тогда говорят, что квадратное уравнение не имеет действительных корней (или что оба корня являются комплексно-сопряженными). В этом случае, обозначая

,

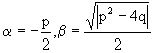общее решение однородного уравнения дается в виде

.

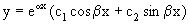Рассмотрим теперь решение неоднородного уравнения

y//+py/+g(y)h(x),

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.





Предыдущая страница реферата | 11  12  13  14  15  16  17  18  19  20  21 | Следующая страница реферата