Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

,

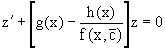являясь линейным однородным дифференциальным уравнением (в нем вместо y взята для удобства переменная z, чтобы не возникло путаницы решений этого уравнения с исходным).

Общее решение этого уравнения, как уже отмечалось ранее, может быть представлено в виде

,

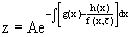где A – произвольная постоянная. Очевидно, 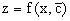является его частным решением, и, следовательно, может быть получено при некотором значении 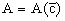, т.е.

.

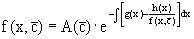Если теперь освободиться от условия фиксирования постоянной 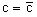, то получаем, что общее решение исходного уравнения имеет вид

.

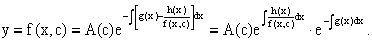В нем второй множитель функция 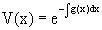является, как нетрудно видеть, частным решением при c=1 однородного линейного уравнения 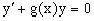. Первый множитель функция 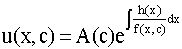представляет общее решение дифференциального уравнения u/v(x)=h(x).

Действительно, подставляя в это уравнение u/x(x,c), получаем тождество

.

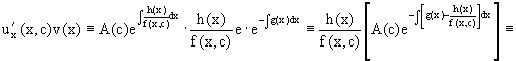
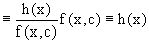Таким образом, показано, что общее решение линейного дифференциального уравнения

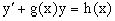
Представляется в виде y=u(x,c)v(x), где v(x) – частное решение однородного уравнения 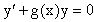, решаемое при c=1, u(x,c) – общее решение уравнения u/v(x)=h(x).

Нетрудно видеть, что в обоих случаях приходится решать уравнение с разделяющимися переменными.

Заметим, что хотя при решении однородного уравнения 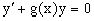бралось частное решение V(x) однородного уравнения v/+g(x)v=0,

Являющегося уравнением с разделяющимися переменными.

На втором этапе определяется решение u(x,c) дифференциального уравнения u/v(x)=h(x),

Также являющегося уравнением с разделяющимися переменными. После их решений общее решение исходного линейного уравнения представляется в виде

Y=u(x,c)v(x).

Пример 1. Решить уравнение

Y/+2y=sinx.

Сначала решаем однородное уравнение v/+2v=0.

Из него получаем

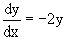или .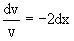

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.





Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата