Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Исключая из уравнений параметр c получаем уравнение кривой y=0, являющейся осью Ox.

Кривая y=0 удовлетворяет дифференциальному уравнению и, следовательно, является его решением. Однако, она не является огибающей, так как не имеет общих точек с интегральными кривыми семейства. Таким образом, являясь решением уравнения, она не является его особым решением.

Далее будут рассмотрены методы решения отдельных типов дифференциальных уравнений.

3. Дифференциальное уравнение первого порядка с разделяющимися переменными.

Определение. Дифференциальное уравнение первого порядка

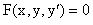
называется уравнением с разделяющимися переменными, если оно может быть представлено в виде 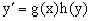или .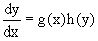

Разнося переменные x и y и их дифференциалы в разные стороны такого уравнения, оно может быть записано в виде

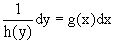(отсюда происходит название данного типа уравнения).

Можно следующую интерпретацию происхождения данного уравнения.

Пусть величина Z является с одной стороны функцией величины y, т.е. z=M(y). С другой стороны величина Z является функцией величины x, т.е. z=g(x). Например, если Z-объем выпуска продукции, то с одной стороны z зависит от величины y – объема основных фондов, с другой стороны z может рассматриваться зависимой от величины x – объема затрачиваемых трудовых ресурсов. Таким образом, через соотношения z=H(y) и z=G(x) одна из величин y или x представляется функцией другой величины x или, соответственно, y. Исходное дифференциальное уравнение отображает эту функциональную связь через дифференциалы функций H(y) и G(x), уравнивая их, т.е. dz=dH(y)=dG(x). Отсюда можно считать, что .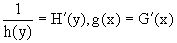

Таким образом, чтобы найти эту функциональную связь в виде y=y(x),x=x(y) или f(x,y)=0, надо проинтегрировать каждую из частей дифференциального уравнения, получая

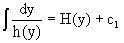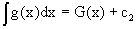, и затем приравнять их H(y)+c1=G(x)+c2 (имея в виду z=H(y)+c1, z=G(x)+c2, и затем z исключается). Вместо двух постоянных c1 и c2 обычно берется одна c=c2-c1, и тогда общее решение дифференциального уравнения записывается в виде

H(y)=G(x)+c.

Если это возможно, из него одна из величин может быть представлена явно функцией другой y=y(x) или x=x(y).

Пример 1. Рассмотрим дифференциальное уравнение получаемое при моделировании процесса распространения информации о новом товаре

.

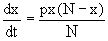Данное уравнение, очевидно, относится к уравнению с разделяющимися переменными. Разнеся переменные x и t и их дифференциалы по разные стороны, уравнение запишем в виде

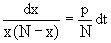или .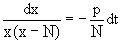

Проинтегрируем каждую из сторон этого уравнения:

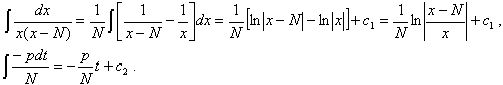
Приравнивая найденные интегралы получаем

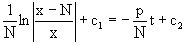или ,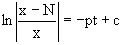

где c=N(c1-c2). Отсюда дале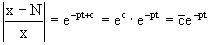е , где 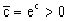. Так как по смыслу задачи 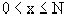, то 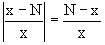, и тогда 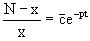. Окончательно общее решение дифференциального уравнения получает вид

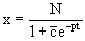, где >0.

Нетрудно проверить, что дискретной и огибающей кривых дифференциальное уравнение не имеет. Однако беря крайние значения для 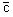равные 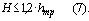, получаем кривые x=N и x=0, являющиеся решениями уравнения, но не особыми.

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.





Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата