Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

А) 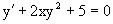является дифференциальным уравнением 1-го порядка;

Б) 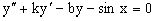является дифференциальным уравнением 2-го порядка;

В) 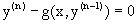является дифференциальным уравнением n-го порядка.

Определение. Решением дифференциального уравнения называется всякая функция y=f(x), которая, будучи подставлена в уравнение, обращает его в тождество.

Например, пусть дано дифференциальной уравнение .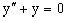

Тогда любая функция вида y=c1sinx+c2cosx, где c1, c2 – произвольные постоянные, является решением этого уравнения.

Действительно, дифференцируя уравнение y=c1sinx+c2cosx дважды по x получаем 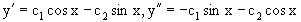. Подставляя выражения для 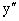и y в левую часть исходного дифференциального уравнения получаем .

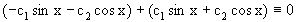Процесс решения дифференциального уравнения называют интегрированием. Поэтому само решение называют еще интегралом уравнения.

Как правило, дифференциальному уравнению отвечает множество решений (смотрите вышеприведенный пример), задаваемых семейством функций y=f(x,c) в явном виде или Ф(x,y,c)=0 в неявном виде. В этих уравнениях с-параметр семейства. Таких параметров, вообще говоря, может быть несколько.

В общем случае обыкновенному дифференциальному уравнению n-го порядка

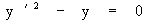отвечает семейство решений, содержащих n параметров.

Определение. Общим решением дифференциального уравнения n-го порядка называется функция y=f(x, c1, c2, …, cn), зависящая от аргумента x и n произвольных постоянных c1, c2, …, cn, которая будучи подставлена в уравнение обращает его в тождество.

Отметим, что эта функция может задаваться и неявным образом, тогда она представляется уравнением Ф(x , y,c1, c2, …, cn)=0.

Общее решение дифференциального уравнения называется также общим интегралом.

Чтобы из общего уравнения выделить некоторое конкретное частное решение дифференциального уравнения, необходимо задать значения для параметров c1, c2 , …, cn. Обычно значения этих произвольных постоянных c1, c2 , …, cn определяются заданием начальных условий: y(x0)=y0, 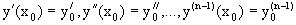. Эти начальные условия дают соответственно n уравнений

,

,

,

………………………………

,

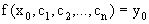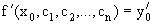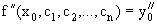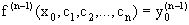решая которые относительно c1, c2 , …, cn находят значения этих постоянных.

Например, для дифференциального уравнения 1-го порядка 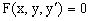общее решение имеет вид y=f(x,c). Тогда начальное условие y(x0)=y0 выделяет из всего семейства интегральных кривых кривую, проходящую через точку M(x0,y0).

Геометрическая интерпретация.

Геометрическое представление решения дифференциального уравнения рассмотрим на примере уравнения 1-го порядка вида .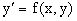

В плоскости введем декартову систему координат с осями x и y. Каждой точке M(x,y) плоскости поставим в соответствие вектор 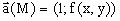, отложенный от точки M.

Таким образом дифференциальное уравнение 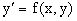порождает в плоскости XOY поле направлений (естественно, указанное поле существует только в области определения функции f(x,y)). Тогда решением дифференциального уравнения будет такая кривая, которая в каждой точке касается вектора поля направляющей.

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата