Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Найти его частное решение при условии .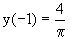

Разрешая уравнение относительно y/, видим, что оно является уравнением с разделяющимися переменными

.

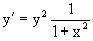Разнося переменные по разные стороны уравнения получаем

.

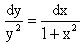Интегрируя каждую из частей этого уравнения, получаем следующее общее решение исходного дифференциального уравнения

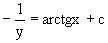или .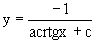

Используя начальное условие 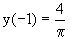, определяем значение константы c для искомого частного решения 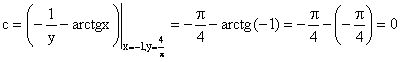. Искомое частное решение дается уравнением .

4. Однородное дифференциальное уравнение первого порядка.

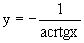Функция f(x,y) называется однородной степени m, если .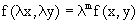

Функция f(x,y) называется однородной нулевой степени, если .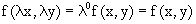

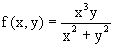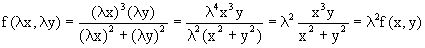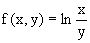Например, функция является однородной второй степени. Действительно, . Функция однородная нулевой степени, так как .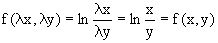

Всякая однородная функция нулевой степени может быть представлена в виде функции от отношения y/x (или отношения x/y). Действительно, пусть f(x,y) – однородная функция нулевой степени, тогда, взяв в качестве 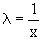, имеем 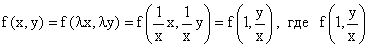может рассматриваться как функция отношения y/x, т.е. .

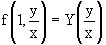Определение. Дифференциальное уравнение первого порядка F(x,y,y/)=0, называется однородным, если оно может быть представлено в виде y/=f(x,y) или 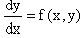., где f(x,y) – однородная функция нулевой степени.

Решение однородного дифференциального уравнения сводится к решению уравнения с разделяющимися переменными заменой y/x=u или y=ux, где u-функция от x.

Подставляя в исходное уравнение 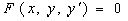и 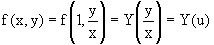, получаем уравнение вида 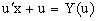или 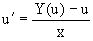, являющиеся с разделяющимися переменными. Если u=g(x,c) или Ф(x,u,c)=0 является его общим решением, то y=xg(x,c) или Ф(x,y/x,c)=0 будет общим решением исходного уравнения.

Пример 1. Рассматривается уравнение

(x2-y2)dx+2xydy=0.

Перепишем его в виде 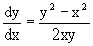. Справа стоит функция однородная нулевой степени. Действительно, 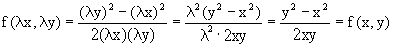. Итак, преобразованное уравнение является однородным дифференциальным уравнением. Решаем его заменой y=ux. Получаем

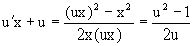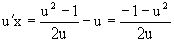или , т.е. .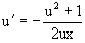

Разделяя переменные приходим к уравнению

.

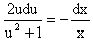Интегрируем левую и правую части этого уравнения:

.

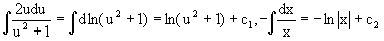Приравнивая найденные интегралы, получаем общее решение вспомогательного дифференциального уравнения относительно переменных x и u

или 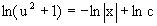, где c>0.

Рекомендуем скачать другие рефераты по теме: собственность реферат, шпаргалки бесплатно скачать.





Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата