Двухфакторная дисперсионная модель имеет вид: xijk=μ+Fi+Gj+Iij+εijk, (15) где xijk - значение наблюдения в ячейке ij с номером k; μ - общая средняя; Fi - эффект, обусловленный влиянием i-го уровня фактора А; Gj - эффект, обусловленный влиянием j-го уровня фактора В; Iij - эффект, обусловленный взаимодействием двух факторов, т.е. отклонение от средней по наблюдениям в ячейке ij от суммы первых трех слагаемых в модели (15); εijk - возмущение, обусловленное вариацией переменной внутри отдельной ячейки. Предполагается, что εijk имеет нормальный закон распределения N(0; с2), а все математические ожидания F*, G*, Ii*, I*j равны нулю. Групповые средние находятся по формулам: - в ячейке:
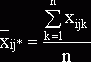по строке:
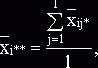
по столбцу:
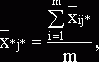
общая средняя:
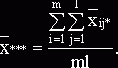
В таблице 1.3 представлен общий вид вычисления значений, с помощью дисперсионного анализа. Таблица 1.3 – Базовая таблица дисперсионного анализа
|
,
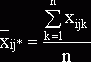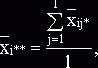
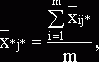
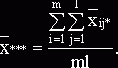
Главная