Элементы планиметрии

Мендель Виктор Васильевич, доцент кафедры геометрии ХГПУ

Цель предлагаемого задания – повторить материал по планиметрии для дальнейшего его использования при решении задач по стереометрии, а также применения при решении олимпиадных задач.

Предлагаемая разработка состоит из двух блоков. В первом изложены основные геометрические конструкции и связанные с ними факты; основные вычислительные формулы и замечательные теоремы, связанные с геометрией треугольника.

Во втором блоке собраны задачи. Начинается этот блок с опорных задач, которые нужно обязательно разобрать. Далее изложены задачи для самостоятельного решения. Они разделены по уровню сложности и по тематике. Некоторые снабжены указаниями к решению.

Вам необходимо внимательно прочитать и повторить материал первого блока. Решить опорные задачи (решения этих задач высылать не надо). Затем вы должны решить из задач для самостоятельного решения необходимый минимум (или больше). Минимальное количество задач по каждому разделу указано в начале каждого раздела. Если в школе учится несколько учащихся Заочной краевой физмат школы, им рекомендуется решать различные задачи.

Оформление решения:

Номер задачи. Краткая запись (текст можно не переписывать). Пояснение всех обозначений (Например: АН – высота из вершины А; ВМ – медиана; l – длина биссектрисы CL и т.п.).

Аккуратный чертеж с четкими обозначениями.

Решение (с необходимыми короткими комментариями. Например: из того, что треугольник ABC – прямоугольный — следует … , из Δ ABC по теореме косинусов выразим сторону BC и т.п.). При оформлении решения допускаются ссылки на материал первого блока.

I. Основные геометрические конструкции, вычислительные формулы и теоремы.

Основные конструкции.

Треугольник с построенными медианами.

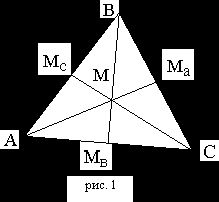Медианы пересекаются в одной точке (центроид, центр тяжести) и делятся этой точкой в отношении 2:1 считая от вершины.

Медиана разбивает треугольник на два равных по площади треугольника.

Медианы разбивают треугольник на шесть равных по площади треугольников.

Площади треугольников АМВ, ВСМ и САМ – равны.

Если точка М лежит внутри треугольника и обладает свойством 4, то это точка пересечения медиан.

Треугольник с построенными высотами.

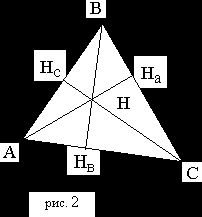Прямые, содержащие высоты треугольника, пересекаются в одной точке (точка пересечения высот, ортоцентр).

Если треугольник остроугольный – Н лежит внутри него, если тупоугольный – вне треугольника, если прямоугольный – совпадает с вершиной прямого угла.

Треугольник АВС и АНВНС – подобны: .

Четырехугольник ВСНВНС вписывается в окружность: ÐВСНВ+ÐНВНСВ=180°.

Четырехугольник АНСННВ вписывается в окружность: ÐА+ÐНСННВ=180°.

Середины сторон треугольника, основания его высот и середины отрезков, соединяющих ортоцентр с вершинами лежат на одной окружности (окружность девяти точек).

Треугольник с построенными биссектрисами.

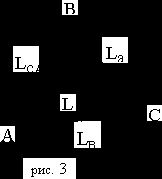Основное свойство биссектрис:  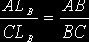(то же верно и для биссектрисы внешнего угла треугольника).

Рекомендуем скачать другие рефераты по теме: дипломная работа персонал, реферат охрана.





1  2  3  4  5  6  7 | Следующая страница реферата