Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Общие внешние (внутренние) касательные двух окружностей пересекаются в точках, лежащих на линии центров.

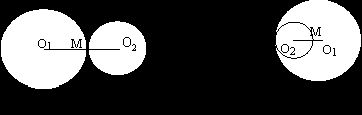Если две окружности касаются, то точка касания лежит на линии центров.

Основные вычислительные формулы.

Теорема косинусов:

Площадь треугольника:

– стороны треугольника, – углы,– высота, – полупериметр,  – радиус описаной окружности,  – радиус вписаной окружности.

Площадь выпуклого четырехугольника: , и  – диагонали,  – угол между ними.

2.4. Площадь выпуклого многоугольника с периметром, описанного вокруг окружности радиуса : .

2.5.Формула Герона для вычисления площади треугольника: , где .

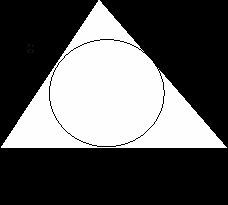2.6.Длина отрезков, на которые делят стороны треугольника точки касания вписаной окружности:, ,

2.7.Теорема Птолемея: во вписаном 4-х угольнике произведение диагоналей равно сумме произведений противоположных сторон: .

2.8.Площадь трапеции: , и  – основания,  – высота трапеции.

2.9.Чтобы найти радиус окружности, описанной вокруг многоугольника, нужно найти радиус окружности, описанной вокруг треугольника, вершинами которого служат три каких-либо вершины данного многоугольника.

3. Некоторые замечательные теоремы планиметрии.

3.1. Теорема Менелая.

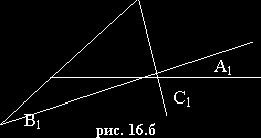Точки А1, В1 и С1 лежат на одной прямой тогда и только тогда, когда .

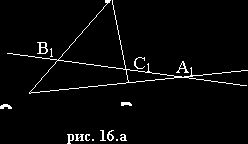
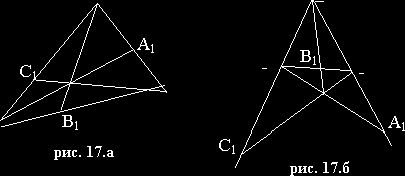3.2.Теорема Чевы.

Прямые АА1, ВВ1 и СС1 пересекаются в одной точке тогда и только тогда, когда

.

3.3.Теорема Пифагора.

3.4. Некоторые свойства прямоугольного треугольника:

 – радиус вписаной окружности

Рекомендуем скачать другие рефераты по теме: дипломная работа персонал, реферат охрана.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата