2.3
В равнобедренном треугольнике отношение разницы между радиусом описанной
окружности и основной высотой к величине первого равно косинусу двойного угла
при основании:
|
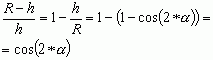
|
(8)
|
Следствие
из теорем 1 и 2:
В
равнобедренном треугольнике отношение радиуса вписанной к радиусу описанной
окружности равно произведению тангенса половинного угла при основании и синуса
двойного угла при основании:
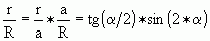 (9)
(9)
В
табл. 1 представлены взаимосвязи между линейными элементами равнобедренного
треугольника (основная высота, половина основания, боковая сторона, радиусы
вписанных и описанных окружностей), выражаемые через тригонометрические
выражения равных углов при основании.
Таблица
1
Соотношения
в равнобедренном треугольнике

 Главная
Главная