Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

так как корни уравнений равны, то уравнения равносильны.

Что и требовалось доказать.

Рассмотрим уравнение

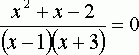ОДЗ этого уравнения {х ≠ 1, х  ≠ -3}

Мы знаем, что дробь равна нулю в том случае, когда ее числитель равен нулю, т.е. х²+х–2=0, а знаменатель не равен 0. Решая уравнение х²+х–2=0, находим корни х1=1, х2 = –2 . Но число 1 не входит в ОДЗ данного уравнения и значит, исходное уравнение имеет один корень  х=-2.

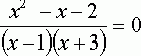
   В этом случае говорят, что уравнение х²+х–2=0, есть следствие уравнения

пусть даны два уравнения:

f1 (x) = g1 (x)     (3)

f2 (x) = g2 (x)     (4)

Если каждый корень уравнения (3) является корнем уравнения (4), то уравнение (4) называют следствием уравнения (3).

Этот факт записывают так:

В том случае, когда уравнение (3) - есть также следствие уравнения (4), эти уравнения равносильны.

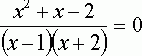
   Два уравнения равносильны в том, и только в том случае, когда каждое из них является следствием другого.

   В приведенном выше примере уравнение – следствие
х²+х–2=0, имеет два корня x1=1 и х2 =-2, а исходное уравнение имеет один корень х=-2. В этом случае корень х=1 называют посторонним для  исходного уравнения      

  

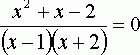
В общем случае корни уравнения-следствия, не являющиеся корнями исходного уравнения, называют посторонними.

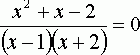
   Итак, если при решении уравнения происходит переход к уравнению – следствию, то могли появиться посторонние корни. В этом случае все корни уравнения-следствия нужно проверить, подставляя их в исходное уравнение. В некоторых случаях выявление посторонних корней облегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ, можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 не входит в ОДЗ уравнения и потому отброшен.

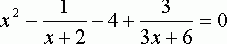
Иногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения

                                                                                                                             ОДЗ которого {х ¹-2},                               

получим уравнение следствие х²-4=0 имеющее два корня х1 = 2,  х2 = -2 корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.

В тех случаях, когда в результате преобразований произошел переход от исходного уравнения к уравнению, не являющемуся его следствием, возможна потеря корней.

Например, уравнение (х+1)(х+3)= х+1     (5)

Имеет два корня. Действительно, перенося все члены уравнения в левую часть и вынося х+1 за скобки, получим (х+1)(х+2)=0, откуда находим х1=-1, х2=-2 .

Если же обе части уравнения (5) разделить («сократить») на х+1, то получим уравнение х+3=1, имеющее один корень х=-2. В результате такого преобразования  корень х=-1 потерян. Поэтому делить обе части уравнения на выражение, содержащее переменную, можно лишь в том случае, когда это выражение отлично от нуля.

Рекомендуем скачать другие рефераты по теме: сочинение егэ, методы изложения.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата