Математическое моделирование ВВЕДЕНИЕ

Различают четыре типа зависимостей между переменными:

1)Зависимость между неслучайными переменными, не требующую для своего изучения применения статистических методов;

2) 1)Зависимость случайной переменной y от неслучайных переменных, исследуемую методами регрессионного анализа;

3) 1)Зависимость между случайными переменными y и xi, изучаемую методами корреляционного анализа;

4) 1)Зависимость между неслучайными переменными, когда все они содержат ошибки измерения, требующую для своего изучения применения конфлюэнтного анализа.

Применение регрессионного анализа для обработки результатов наблюдений позволяет получить оценку влияния переменных, рассматриваемых в качестве аргументов (независимых переменных) на переменную, которая считается зависимой от первых.

Курсовая работа направлена на освоение методов регрессионного анализа в процессе разработки математического описания исследуемого процесса или явления. Курсовая работа предусматривает обработку экспериментальных данных и поиск наиболее удовлетворительной гипотезы взаимосвязи между функцией и аргументами.

В качестве таких гипотез рассматриваются линейная и нелинейная регрессионные модели, каждая из которых может быть парной (только две переменных - функция и аргумент) или множественной (одна функция и несколько аргументов).

Относительно закона изменения независимых переменных xi не делается никаких ограничений –

ЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ

Для нахождения теоретической линии регрессии по данным производственных замеров или специально поставленных экспериментов применяется метод наименьших квадратов, с помощью которого путем определенных вычислений находится уравнение y = f(x), соответствующее взаимосвязи рассматриваемых параметров. А именно, отыскивается теоретическая линия регрессии у по х, занимающая в корреляционном поле такое положение, при котором выполняется требование, чтобы сумма квадратов расстояний от этой линии до каждой точки в корреляционном поле являлась минимальной.

При изображении корреляционного поля на графике по оси у откладывают значения функции, а по оси х — значения аргумента . Теоретическая линия регрессии у по х должна быть внесена в корреляционное поле таким образом, чтобы соблюдался принцип наименьших квадратов:

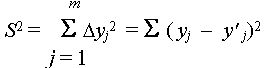
где j— порядковый номер точки в исходном числовом материале:

у j—измеренное значение функции для определенного значения аргумента (х);

y'/--расчетное значение функции при заданной величине аргумента (х) в соответствии с теоретической их взаимосвязью. В случае линейной зависимости

y'j = a + b x j. (2)

Задача сводится к отысканию коэффициентов регрессии а и b уравнения (2), т. е. заранее установлено, что рассматриваемые параметры у и х связаны линейной зависимостью по уравнению (2).

Величина D yj представляющая собой расстояние от каждой точки корреляционного поля до теоретической линии регрессии, определяется из уравнения

D yj = yj - ( a + b x j ) (3)

где x j— параметр х, соответствующий измеренному значению у j.

Для определения численных значений коэффициентов регрессии a и b, исходя изпринципа наименьших квадратов отклонений, нужно приравнять нулю частные производные функции S 2 по a и b:

¶ S 2/ ¶ a = ¶ ( S D yj ) 2 / ¶ a = 0, ( 4 ) ¶ S 2/ ¶ b = ¶ ( S D yj ) 2 / ¶ b = 0 ( 5 )

Выполнив необходимые преобразования, получим систему двух уравнений с двумя неизвестными для определения a и b:

S y = m a + b S x S yx = a S x + b S x 2 . ( 6 )

Решая систему уравнений относительно a и b, находим численные знаяения коэффициентов регрессии. Величины S y, S x, S yx, S x2 находятся непосредственно по данным производственных измерений, которые заданы в курсовой работе.

Величина свободного члена уравнения регрессии (2), или коэффициента а равна функции у при x = 0.

Коэффициент b в уравнении регрессии характеризует изменение функции у при изменении аргумента х на единицу. и графически отражает угол наклона линии уравнения регрессии

При решении практических задач регрессионного анализа возникает вопрос об оценке тесноты исследуемой взаимосвязи, т. е. насколько полученные на основе обработки производственных или лабораторных данных уравнения регрессии достоверны. В случае парной линейной корреляции в качестве оценки тесноты связи используют обычно коэффициенткорреляции, который рассчитывается по формуле:

r = (XY - X * Y)/( s x * s y ). ( 7 )

Числитель выражения для коэффициента корреляции r представляет собой разность между средним значением произведения XY и произведением средних значений X * Y измеренных значений параметров x и y исходной информации. Знаменатель равен произведению средних квадратических отклонений значений параметров у и х от своих средних. Средние квадратические отклонения (стандартные отклонения) рассчитываются по формулам:

s x = {[ S ( x j - X ) 2 ]/ m }1/2 ( 8 ) s y = {[ S ( y j - Y ) 2 ]/ m }1/2 . ( 9 )

Квадраты средних квадратических отклонений y и х (s x 2 и s y 2 ) называются дисперсиями

Рекомендуем скачать другие рефераты по теме: профессиональные рефераты, бесплатные доклады.





1  2  3  4  5  6 | Следующая страница реферата