Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата

Уравнение такой поверхности наилучшим образом опишет взаимосвязь у, X 1 и Х2.

y = a + b1 x1 + c1 x12 + b 2 x 2 + c 2 x22 . ( 38 ) ,

Для определения коэффициентов такого уравнения используем систему пяти уравнений с пятью неизвестными.

S y = m a + b1 S x1 + с1 S x12 + b2 S x2 + с2 S x22 S yx1 = a S x1 + b1 S x12 + с1 S x13 + b2 S x1 x2 + с2 S x22 x1 S yx1 2 = a S x12 + b1 S x13 + с1 S x14 + b2 S x2. x12+с2 S x 22x12 S yx2 = a S x2 + b1 S x1 x2+ с1 S x12 x 2 + b2 S x22 + с2 S x23 S yx22 = a S x22 + b1 S x1 x22 + с1 S x12 x22+ b2 S x23. + с2 S x24 (39)

Если все точки корреляционного пространства находятся на расчетной поверхности, то множественное корреляционное отношение будет равно единице. При этом связь между функцией у и аргументами x1 и x2 будет функциональной. По мере удаления точек от расчетной поверхности этот показатель будет уменьшаться, приближаясь к нулю.

При переходе к анализу криволинейных связей возникает проблема выбора типа кривой, с помощью которой выполняется аппроксимация каждой пары рассматриваемых переменных. Для монотонно меняющегося процесса в сравнительно небольших интервалах изменения параметров, каким является металлургический процесс, можно без значительной ошибки аппроксимировать все существующие связи Xi—Хе и у—Xi с помощью полиномов второй степени. Такое допущение намного упрощает методику расчета, , но в то же время сохраняет рассмотренные выше преимущества, присущие криволинейной аппроксимации. На основе сделанного допущения можно рассчитать уравнение множественной криволинейной регрессии вида:

y = a + S b i x i + S c i xi 2 ( 40 )

где b и c— коэффициенты регрессии при i-том аргументе (1 =1, 2,...,п);

n—число аргументов в регрессионной модели;

а—свободный член уравнения регрессии.

Коэффициенты а, b и c, так же как и прежде, находятся методом наименьших квадратов из системы уравнений, которая в данном случае будет большей по сравнению с системой для определения коэффициентов множественной линейной регрессии. Количество неизвестных (а, b и c), равное числу уравнений в случае множественной криволинейной регрессии, составит z = 2 n + 1, где п—число аргументов в корреляционной модели. Таким образом, если для определения уравнения множественной линейной корреляции с десятью аргументами необходимо решить систему из 11 уравнений с 11 неизвестными {а и 10 x), то для нахождения уравнения с десятью аргументами необходимо решить систему из 21 уравнения с 21 неизвестным .

Частное уравнение регрессии в этом случае имеет вид

уx i =а' + b i x i + c ixi2, (41) .

причем свободный член этого уравнения а ' для каждой связи у— x i имеет свое численное значение, отличное от свободного члена а в уравнении множественной регрессии ( ), ( ), а значения коэффициенты регрессии b i и c i те же. Свободный член частного уравнения регрессии в данном случае рассчитывается по формуле

a'i = a + S b 1- (n - i ) X 1- (n - i ) + S c 1- (n - i ) X 21- (n - i )( 42 )

где a — свободный член уравнения множественной регрессии.

Второй член правой части уравнения представляет собой сумму произведений средних значений каждого аргумента, кроме 1-того, на его коэффициент регрессии bi, а третий член правой части уравнения представляет собой сумму произведений квадратов средних значений каждого аргумента, кроме t-того, на его коэффициент регрессии c i. Коэффициенты регрессии b и c взяты из уравнения множественной регрессии . Таким образом, из уравнения множественной регрессии может быть получен ряд уравнений частной регрессии (по числу аргументов п в корреляционной модели), с помощью которых определяются характер индивидуальных взаимосвязей функции и каждого аргумента.

Оценкой тесноты частной корреляционной связи в данном случае служит частное корреляционное отношение. Этот показатель рассчитывается аналогично парному корреляционному отношению .

ЗАДАНИЕ НА ВЫПОЛНЕНИЕ КУРСОВОЙ РАБОТЫ

Задание на выполнение курсовой работы состоит из краткого текста, поясняющего существо приводимых в задании групп исходных данных и самих групп исходных данных. Среди этих данных имеется несколько аргументов и одна функция. В задача курсовой работы входит проверка гипотез возможных связей между аргументами и функцией. Критерием правильности одной из гипотез является показатель тесноты связи. Это либо коэффициент парной или частной корреляции, либо парное или частное корреляционное отношение. После статистической обработки исходных данных проводится сравнение полученных показателей и делаются выводы о правомерности одного из предположений о характере связей.

СОСТАВ, ОБЪЕМ И СОДЕРЖАНИЕ КУРСОВОЙ РАБОТЫ

Курсовая работа включает теоретическую часть, в которой приводится описание методов регрессионного анализа, применяемых в данной работе.

Следующий раздел предусматривает предварительную статистическую обработку данных для их последующего рационального использования. Автор работы указывает на необходимость вычисления средних значений аргументов, средних квадратов аргументов, средних значений третьей и четвертой степени и т.д., после чего составляется таблица обработки исходных данных. Вид таблицы приведен ниже.

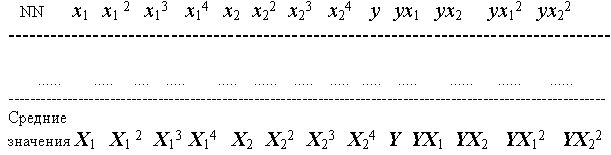
Правильно составленная таблица позволяет легче справляться с вычмслением различнхы ситуаций в процессе решения разделов регрессионного анализа.

ОФОРМЛЕНИЕ КУРСОВОЙ РАБОТЫ

Курсовая работа офрмляется следующим образом.

- Титульный лист с указанием фамилии , имени, отчества студента и фамилии преподавателя

- Оригинал задания на выполнение курсовой работы

- Аннотация курсовой работы

- Оглавление работы

Теоретическая часть

Практическая часть работы

Выводы

Рекомендуем скачать другие рефераты по теме: профессиональные рефераты, бесплатные доклады.





Предыдущая страница реферата | 1  2  3  4  5  6 | Следующая страница реферата