Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поэтому, для того чтобы структура раствора, состоящего из n компонент, была определена, достаточно знать концентрацию (n-1)-й компоненты. Если известны концентрации сA , сB и сC компонент, составляющих данную смесь, то ее объем можно разделить на объемы отдельных компонент (рис. 1):

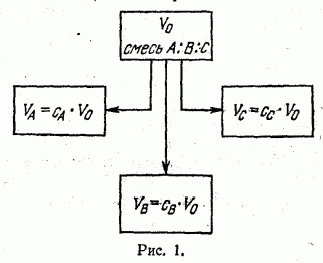
V0=cAV0+cBV0+cCV0.                (формула 1)

Объемным процентным содержанием компоненты А называется величина

рА=cA100% ,                  (**)

т. е. концентрация этого вещества, выраженная в процентах.

Если известно процентное содержание: вещества А, то его концентрация находится по формуле

cA=рА/100% .

Так, например, если процентное содержание составляет 70%, то соответствующая концентрация равна 0,7. Процентному содержанию 10% соответствует концентрация 0,1 и т.д.

Таким же способом определяются и весовые (массовые) концентрация и процентное содержание, а именно как отношение веса (массы) чистого вещества А

в сплаве к весу (массе) всего сплава. О какой концентрации, объемной или весовой, идет речь в конкретной задаче, всегда ясно из ее условия.

Встречается сравнительно немного задач, в которых приходится пересчитывать объемную концентрацию на весовую или наоборот. Для того чтобы это сделать, необходимо знать удельные веса компонент, составляющих раствор или сплав. Рассмотрим для примера двухкомпонентную смесь с объемными концентрациями компонент с1 и с2 (с1+с2=1) и удельными весами компонент d1 и d2. Вес смеси может быть найден по формуле

G=V1d1+V2d2

в которой V1 и V2 - объемы составляющих смесь компонент. Весовые концентрации компонент находятся из равенств

k1 =V1d1 / (V1d1 +V2d2)=c1d1 /(c1d1 +c2d2)=c1d1 /(c1(d1 -d2)+d2) ,

k2 =V2d2 / (V1d1 +V2d2)=c2d2 /(c1d1 +c2d2)=c2d2 /(d1 +c2 (d2 -d1)) ,

которые определяют связь этих величин с объемными концентрациями.

Как правило, в условиях задач рассматриваемого типа встречается один и тот же повторяющийся элемент: из двух или нескольких смесей, содержащих компоненты A1, А2, А3, ..., An, составляется новая смесь путем перемешивания исходных смесей, взятых в определенной пропорции. При этом требуется найти, в каком отношении компоненты A1, А2, А3, ..., An войдут в получившуюся смесь.

Для решения этой задачи удобно ввести в рассмотрение объемное или весовое количество каждой смеси, а также концентрации составляющих их компонент A1, А2, А3, ..., An. С помощью концентраций нужно “расщепить” каждую смесь на отдельные компоненты, как это сделано в формуле (1), а затем указанным в условии задачи способом составить новую смесь. При этом легко подсчитать, какое количество каждой компоненты входит в получившуюся смесь, а также полное количество этой смеси. После этого определяются концентрации компонент A1, А2, ..., An в новой смеси.

Проиллюстрируем сказанное выше на примере следующей задачи.

Задача1. Имеются два куска сплава меди и цинка с процентным содержанием меди р% и q% соответственно. В каком отношении нужно взять эти сплавы чтобы, переплавив взятые куски вместе, получить сплав, содержащий r% меди?

Решение. Составим иллюстративный рисунок к этой задаче (рис. 2). Концентрация меди в первом сплаве равна р/100, во втором сплаве q/100.

Если первого сплава взять х кг, а второго у кг, то с помощью концентраций (ясно, что речь идет о весовых концентрациях) можно “расщепить” эти количества на отдельные составляющие:

х=хр/100 (кг меди) +x(1-p/100) (кг цинка)

и

Рекомендуем скачать другие рефераты по теме: оформление доклада, онегин сочинение.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата