Методы решения уравнений в странах древнего мира

История алгебры уходит своими корнями в древние времена. Задачи, связанные с уравнениями, решались ещё в Древнем Египте и Вавилоне. Теория уравнений интересовала и интересует математиков всех времён и народов.

В Древнем Египте и Вавилоне использовался метод ложного положения (“фальфивое правило”)

Уравнение первой степени с одним неизвестным можно привести всегда к виду ах + Ь == с, в котором а, Ь, с — целые числа. По правилам арифметических действий ах = с — b,

Если Ь > с, то с — b число отрицательное. Отрицательные числа были египтянам и многим другим более поздним народам неизвестны (равноправно с положительными числами их стали употреблять в математике только в семнадцатом веке).

Для решения задач, которые мы теперь решаем уравнениями первой степени, был изобретен метод ложного положения.

В папирусе Ахмеса 15 задач решается этим методом. Решение первой из них позволяет понять, как рассуждал автор.

Египтяне имели особый знак для обозначения неизвестного числа, который до недавнего прошлого читали “хау” и переводили словом “куча” (“куча” или “неизвестное количество” единиц). Теперь читают немного менее неточно: “ага”.

bqt задача № 24 сборника Ахмеса:

“Куча. Ее седьмая часть ('подразумевается: “дают в сумме”) 19. Найти кучу”.

Запись задачи нашими знаками:

Решение Ахмеса может быть представлено в наших символах в следующих четырех столбцах:

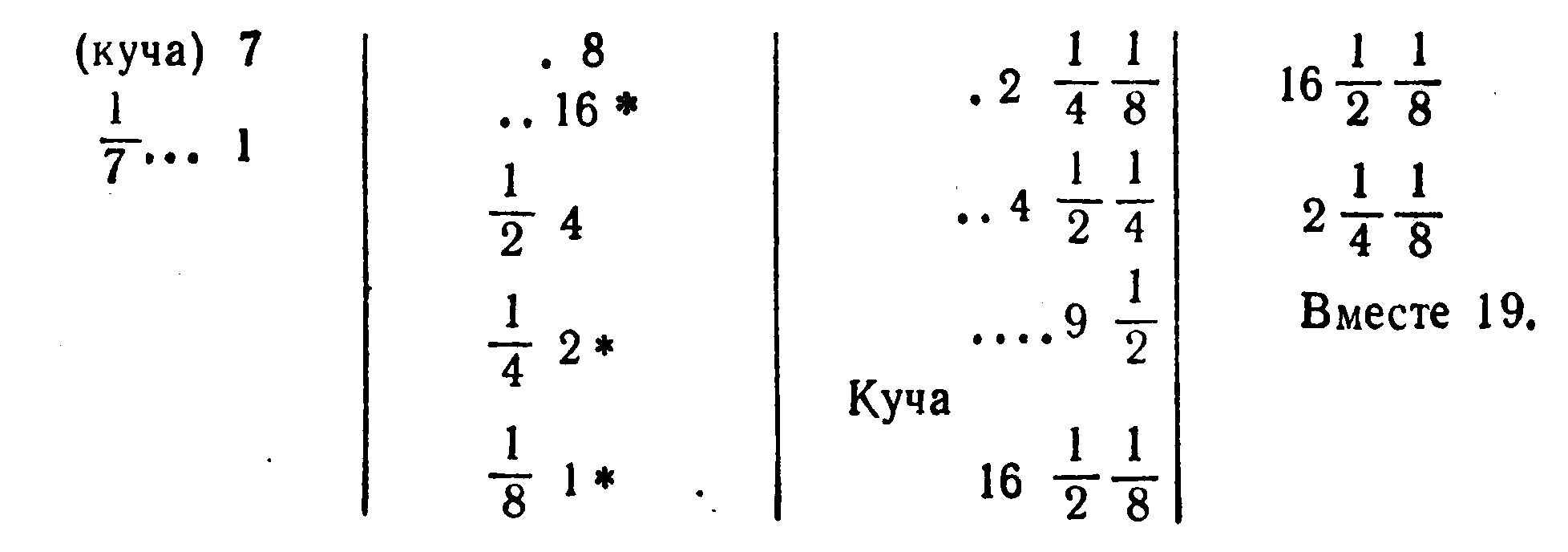
Во многих задачах в начале или в конце встречаются слова: “Делай как делается”, другими словами: “Делай, как люди делают”.

Смысл решения Ахмеса легко понять.

Делается предположение, что. куча есть 7; тогда ее часть есть 1. Это записано в первом столбце.

Во втором столбце записано, что при предположении х=7 куча и ее часть дали бы 8 вместо 19. Удвоение предположения дает 16. Автор, в уме очевидно, прикидывает, что дальше удваивать предположение нельзя, так как тогда получится больше 19. Он записывает 16, ставит перед числом две точки для обозначения удвоения первоначального предположения и отмечает значком (у нас — звездочкой) результат; для получения в сумме 19 первоначальное предположение надо умножить -на 2 с некоторым добавлением, так как для получения точного результата, 19, не хватает еще 19—16=3. Ахмес находит от 8, получает 4. Так как это больше нехватки 3, то на предположение умножить нельзя. Но от 8 есть 2, от восьми 1. Ахмес видит, что и первоначального результата дают точно те 3 единицы, которых не хватало. Отметив и значками, Ахмес убедился, что первоначальное предположение для кучи (7) надо помножить на

Умножение числа 7 на смешанное число Ахмес заменяет умножением смешанного числа на 7. В третьем столбце выписаны: часть искомой кучи есть , удвоенное это число: и учетверенное: . Сумма этих трех чисел, равная числу , есть произведение первоначального предположения 7 на .

Итак, куча равна .

В последнем столбце Ахмес делает проверку, складывая полученное значение для кучи и его части . В сумме получается 19, и решение заканчивается обычным для автора заключением: “Будет хорошо”.

Способ решения, примененный Ахмесом, называется методом одного ложного положения. При помощи этого метода решаются уравнения вида ах == b. Его применяли как египтяне, так и вавилоняне.

У разных народов применялся метод двух ложных положений. Арабами этот метод был механизирован и получил ту форму, в которой он перешел в учебники европейских народов, в том числе в “Арифметику” Магницкого. Магницкий называет способ решения “фальшивым правилом” и пишет о части своей книги, излагающей этот метод:

Рекомендуем скачать другие рефераты по теме: сочинение на тему онегин, шпаргалки по гражданскому праву.

1  2  3  4  5  6  7  8  9 | Следующая страница реферата