Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата



Диофантовы уравнения.

Задача Диофанта №80 (Из II книги его “Арифметики”)

Найти 2 таких числа, чтобы сумма квадрата каждого из них с другим искомым числом дала полный квадрат,

Решение Диофанта

Пусть первое число (I) будет s. Чтобы квадрат его •при прибавлении второго числа дал квадрат, второе число должно быть 2s + 1, так как в таком случае выполняется требование задачи: квадрат первого числа. сложенный со вторым, дает

s2 + 2s + 1, то есть полный квадрат (s + 1)2.

Квадрат второго числа, сложенный с первым, должен также дать квадрат, то есть число (2s + I)2 + s, равное

4s2 + 5s + 1 == t2

Положим, что t = 2s — 2; тогда t2 = 4s2 — 8s + 4. Это выражение должно равняться 4s2 + 5s + 1. Итак, должно быть:

4s2 — 8s + 4 == 4s2 + 5s + l откуда s=

Значит, задаче удовлетворяют числа:

.

 

Проверка;

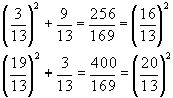
Почему Диофант делает предположение, что t==2s—2, он не объясняет. Во всех своих задачах (в дошедших до нас шести книгах его их 189) он делает то или другое предположение, не давая никакого обоснования.

Вообще содержание 6 книг таково:

В “Арифметике” 189 задач, каждая снабжена одним или несколькими решениями. Задачи ставятся в общем виде, затем берутся конкретные значения входящих в нее величин и даются решения.

Задачи книги I в большинстве определенные. В ней имеются и такие, которые решаются с помощью систем двух уравнений с двумя неизвестными, эквивалентных квадратному уравнению. Для его разрешимости Диофант выдвигает условие, чтобы дискриминант был полным квадратом. Так, задача 30— найти таких два числа, чтобы их разность и произведение были заданными числами,— приводится к системе

х — у = а, х = b.

Диофант выдвигает “условие формирования”: требуется, чтобы учетверенное произведение чисел, сложенное с квадратом разности их, было квадратом, т. е. 4b + а2 = с2.

В книге II решаются задачи, связанные с неопределенными уравнениями и системами таких уравнений с 2, 3, 4, 5, 6 неизвестными степени не выше второй.

Диофант применяет различные приемы. Пусть необходимо решить неопределенное уравнение второй степени с двумя неизвестными f2 (х, у) ==0. Если у него есть рациональное решение (x0, y0), то Диофант вводит подстановку

x = x0 + t,

y = y0 + kt,

Рекомендуем скачать другие рефераты по теме: сочинение на тему онегин, шпаргалки по гражданскому праву.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата