Многочлены над кольцом классов вычетов

| Категория реферата: Рефераты по математике
| Теги реферата: доклад по обж, сочинение
| Добавил(а) на сайт: Rytov.

Предыдущая страница реферата | 1 2 3 4 5 6 7 | Следующая страница реферата

Доказательство. Пусть f(x) делится на , т.е. . Тогда .

Пусть . Тогда в равенстве будет , т.е. . Следствие полностью доказано.

Теорема 3. Число корней ненулевого многочлена не превосходит его степени.

Доказательство. Докажем это утверждение с помощью индукции по степени многочлена. Многочлен нулевой степени вообще не имеет корней, так что для него утверждение теоремы справедливо. Предположим теперь, что утверждение теоремы справедливо для всех многочленов степени , и докажем его для любого многочлена f(x) степени n. Предположим, рассуждая от противного, что x1, x2, ..., xm - корни многочлена f(x), причем . По теореме Безу, f(x) делится на , т.е. , где g(x) - некоторый многочлен степени . Элементы x2..., xm кольца K являются корнями многочлена g(x). В самом деле, при имеем: . Так как , а кольцо K не имеет делителей нуля, то . Таким образом, многочлен g(x) имеет не менее чем корней, что противоречит предположению индукции, поскольку . Теорема доказана.

Следствие. Многочлен степени не выше n однозначно определяется своими значениями в точках.

Иначе говоря, существует не более одного многочлена степени не выше n, принимающего в данных (различных) точках данные значения y1, y2, ..., yn+1.

Доказательство. Предположим, что f(x), g(x) - два многочлена степени не выше n, принимающие одинаковые значения в точках . Рассмотрим многочлен . Степень этого многочлена также не выше, чем n. Так как , то при , т.е. - корни многочлена h(x). Согласно теореме 3 h(x) = 0, т.е. f(x) = g(x).

Теорема 4. Если кольцо K бесконечно, то равенство функций, определяемых двумя многочленами из кольца K[x], влечет за собой равенство самих многочленов.

Доказательство. Пусть многочлены определяют одинаковые функции. Это означает, что для любого . Обозначим через n наивысшую из степеней многочленов f(x), g(x). Так как кольцо K бесконечно, то в нем найдутся различных элементов . Согласно нашему предположению, многочлены f(x) и g(x) принимают одинаковые значения в каждой из точек (как и вообще в любой точке). Следствие теоремы 3 позволяет сделать отсюда вывод, что .

Для конечного кольца K утверждение теоремы 4 неверно. Однако при некоторых дополнительных предположениях и в этом случае оказывается возможным из равенства функций, определяемых двумя многочленами, сделать вывод о равенстве самих многочленов.

6. Вычисление наибольшего общего делителя.

Наибольший общий делитель двух многочленов f и g из кольца R[x] многочленов над полем R может быть найден при помощи алгоритма Евклида. Алгоритм Евклида нахождения наибольшего общего делителя состоит в следующем. Сначала делят с остатком многочлен f на многочлен g, затем многочлен g - на остаток от первого деления, затем остаток от первого деления - на остаток от второго деления и т.д., пока не получится нулевой остаток. Это дает следующую цепочку равенств:

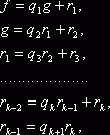(9)

причем , поэтому процесс деления конечен. Пусть , т.е. f и g принадлежат одному и тому же главному идеалу . Поэтому их разность , т.е. . Аналогично можно доказать, что , и т.д. Таким образом, . Из последнего равенства (21) следует, что , тогда . Поэтому . Следовательно, по теореме 14 , т.е. . Таким образом, последний ненулевой остаток (т.е. rk) и есть наибольший общий делитель многочленов f и g.

Пример. В кольце многочленов с действительными коэффициентами найдем наибольший общий делитель многочленов , . Делим f на g:

Для удобства умножим полученный остаток на . При этом последующие остатки также умножатся на некоторые числа, отличные от нуля, что несущественно при нахождении наибольшего общего делителя, так как он находится с точностью до константы. Выполним второе деление: