Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата

Параметр  определяется как .

Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле

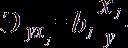
Для расчета частных коэффициентов эластичности применяется следующая формула:

.

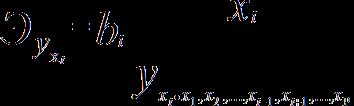Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:

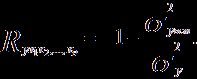
Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:

 

Индекс множественной корреляции для уравнения в стандартизированном масштабе можно записать в виде

При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:

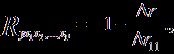
 ---- определитель матрицы парных коэффициентов корреляции;

 ------ определитель матрицы межфакторной корреляции.

Частные коэффициенты (или индексы) корреляции, измеряющие влияние на y фактора  при неизменном уровне других факторов, можно определить по формуле:

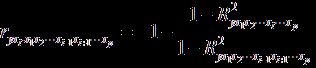
или по рекуррентной формуле:

.

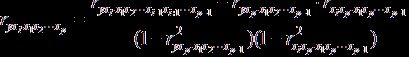Частные коэффициенты корреляции изменяются в пределах от –1 до 1.

Качество построенной модели в целом оценивает коэффициент (индекс) детерминации. Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции:

Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:

Рекомендуем скачать другие рефераты по теме: реферат менеджмент, сочинение описание.





Предыдущая страница реферата | 1  2  3  4  5  6  7 | Следующая страница реферата