Некоторые главы мат. анализа
| Категория реферата: Рефераты по математике
| Теги реферата: контрольная 6 класс, дипломная работа школа
| Добавил(а) на сайт: Rjabec.
Предыдущая страница реферата | 15 16 17 18 19 20 21 22 23 24 25 | Следующая страница реферата
Построив гистограмму мы получили аналог кривой распределения по которой можем выдвинуть гипотезу о законе распределения. Выровнять статистическое распределение с помощью закона о котором выдвинули гипотезу, для этого нужно статист. среднее mx* и статистическую дисперсию Dx* .
Которые находим как
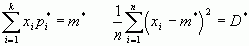
Естественной оценкой для мат. ожидания является среднее арифметическое значение :
.
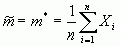Посмотрим, является ли эта оценка не смещенной , для этого найдем ее мате-матическое ожидание :
,
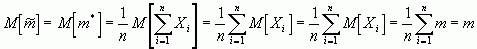то есть оценка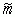 
для m является несмещенной.
Найдем дисперсию этой оценки :
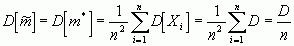
Эффективность или неэффективность оценки зависит от вида закона распределения случайной величины X .Если распределение нормально, то оценка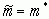 
для мат. ожидания m является и эффективной.
Перейдем к оценке для дисперсии D. На первый взгляд наиболее естественной представляется статистическая дисперсия D*, то есть среднее арифметическое квадратов отклонений значений Xi от среднего :
.
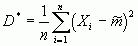Проверим состоятельность этой оценки, выразив ее через среднее арифметическое квадратов наблюдений:
.
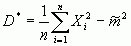, где правая часть есть среднее арифметическое значений случайной величины X2 сходится по вероятности к ее мат. ожиданию: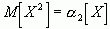 
. Вторая часть сходится по вероятности к 
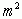; вся величина сходится по вероятности к 
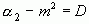. Значит, оценка состоятельна.
Проверим ее на несмещенность, подставив в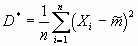 
вместо 
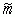его выражение и произведем действия:
.
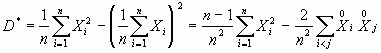Так как D* не зависит от выбора начала координат то отцентрируем все случайные величины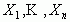 
. Тогда
.
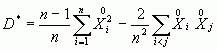Найдем мат. ожидание величины D*:
.
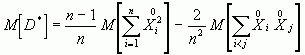Но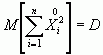 
,
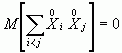, и получаем:
.
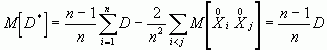Отсюда видно, что величина D* не является несмещенной оценкой для дисперсии D; ее мат. ожидание не равно D, а несколько меньше. Пользуясь оценкой D* вместо D, будет проходить систематическая ошибка в меньшую сторону, чтобы ее ликвидировать введем поправку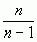 
тогда мы получим несмещенную оценку для дисперсии:
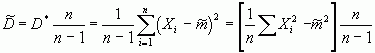
При больших n поправочный коэффициент 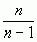становится близким к единицы, и его применение теряет смысл. Поэтому в качестве приближенных значени (оценок) этих характеристик нужно взять:
,
.
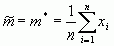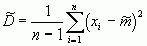Упорядоченная выборка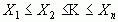 
где n=100 количество замеров :
|
70.1 |
74.7 |
79.1 |
79.4 |
80.0 |
82.0 |
82.2 |
83.4 |
83.8 |
85.0 |
||
|
86.1 |
86.2 |
86.3 |
86.5 |
86.6 |
86.7 |
86.9 |
87.2 |
88.2 |
88.4 |
||
|
88.6 |
88.7 |
89.4 |
90.4 |
90.8 |
90.9 |
91.1 |
91.3 |
93.1 |
93.7 |
||
|
94.5 |
94.7 |
94.7 |
94.8 |
94.9 |
94.9 |
95.1 |
95.2 |
95.3 |
Категории:Предыдущая страница реферата | 15 16 17 18 19 20 21 22 23 24 25 | Следующая страница реферата Поделитесь этой записью или добавьте в закладки |
|
Главная