
–Э–µ–ї–Њ–Ї–∞–ї—М–љ–∞—П –Ї—А–∞–µ–≤–∞—П –Ј–∞–і–∞—З–∞ –і–ї—П —Г—А–∞–≤–љ–µ–љ–Є—П —Б–Љ–µ—И–∞–љ–љ–Њ–≥–Њ —В–Є–њ–∞ —В—А–µ—В—М–µ–≥–Њ –њ–Њ—А—П–і–Ї–∞ —Б –Ї—А–∞—В–љ—Л–Љ–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞–Љ–Є
| –Ъ–∞—В–µ–≥–Њ—А–Є—П —А–µ—Д–µ—А–∞—В–∞: –†–µ—Д–µ—А–∞—В—Л –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ
| –Ґ–µ–≥–Є —А–µ—Д–µ—А–∞—В–∞: –±–µ—Б–њ–ї–∞—В–љ—Л–µ –і–Є–њ–ї–Њ–Љ—Л, —Б–Ї–∞—З–∞—В—М –Ї–Њ–љ—В—А–Њ–ї—М–љ—Г—О
| –Ф–Њ–±–∞–≤–Є–ї(–∞) –љ–∞ —Б–∞–є—В: Bol'shakov.
–Я—А–µ–і—Л–і—Г—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞ | 1 2 3 4 5 6 | –°–ї–µ–і—Г—О—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞
–Ы–µ–≥–Ї–Њ
–Ј–∞–Љ–µ—В–Є—В—М, —З—В–Њ —Д—Г–љ–Ї—Ж–Є—П ![]() ¬†–Є –≤ —В–Њ—З–Ї–µ x=0 –Њ–±—А–∞—Й–∞–µ—В—Б—П –≤ –љ—Г–ї—М –њ–Њ—А—П–і–Ї–∞ –≤—Л—И–µ e, –∞
–њ—А–Є x=1 –Љ–Њ–ґ–µ—В –Њ–±—А–∞—Й–∞—В—М—Б—П –≤ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М –њ–Њ—А—П–і–Ї–∞ –≤—Л—И–µ (1-e)
–Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ x –Є (1-x) —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ш–Ј —А–∞–≤–µ–љ—Б—В–≤–∞ (20) –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ
–Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д—Г–љ–Ї—Ж–Є—П
¬†–Є –≤ —В–Њ—З–Ї–µ x=0 –Њ–±—А–∞—Й–∞–µ—В—Б—П –≤ –љ—Г–ї—М –њ–Њ—А—П–і–Ї–∞ –≤—Л—И–µ e, –∞
–њ—А–Є x=1 –Љ–Њ–ґ–µ—В –Њ–±—А–∞—Й–∞—В—М—Б—П –≤ –±–µ—Б–Ї–Њ–љ–µ—З–љ–Њ—Б—В—М –њ–Њ—А—П–і–Ї–∞ –≤—Л—И–µ (1-e)
–Њ—В–љ–Њ—Б–Є—В–µ–ї—М–љ–Њ x –Є (1-x) —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ. –Ш–Ј —А–∞–≤–µ–љ—Б—В–≤–∞ (20) –Њ–і–љ–Њ–Ј–љ–∞—З–љ–Њ
–Њ–њ—А–µ–і–µ–ї—П–µ—В—Б—П —Д—Г–љ–Ї—Ж–Є—П ![]() :
:
![]()  (21)
 (21)
–£—З–Є—В—Л–≤–∞—П
–Ј–љ–∞—З–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є ![]() ¬†–Є–Ј —А–∞–≤–µ–љ—Б—В–≤–∞ (21), –≤ –Є–љ—В–µ–≥—А–∞–ї–∞—Е –≤ –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є
(16) –њ–Њ–ї—Г—З–∞–µ–Љ:
¬†–Є–Ј —А–∞–≤–µ–љ—Б—В–≤–∞ (21), –≤ –Є–љ—В–µ–≥—А–∞–ї–∞—Е –≤ –њ—А–∞–≤–Њ–є —З–∞—Б—В–Є
(16) –њ–Њ–ї—Г—З–∞–µ–Љ:
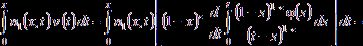
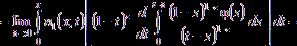
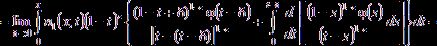
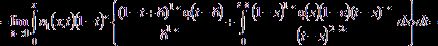
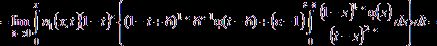
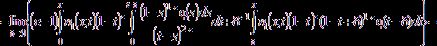
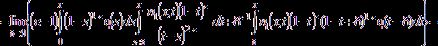
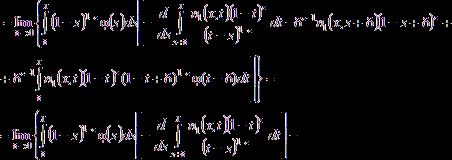
![]()
![]()
![]() .
.
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ
![]() . (22)
. (22)
–Ґ–Њ–≥–і–∞ –Њ–Ї–Њ–љ—З–∞—В–µ–ї—М–љ–Њ –Є–Љ–µ–µ–Љ:
![]() .
.
–Р–љ–∞–ї–Њ–≥–Є—З–љ–Њ –љ–∞—Е–Њ–і–Є–Љ, —З—В–Њ
![]() ,
,
–≥–і–µ
–Њ–±–Њ–Ј–љ–∞—З–µ–љ–Њ ![]() , (23)
, (23)
![]() ; (24)
; (24)
![]() . (25)
. (25)
–Ш—Б–њ–Њ–ї—М–Ј—Г—П –Є–Ј–≤–µ—Б—В–љ–Њ–µ —В–Њ–ґ–і–µ—Б—В–≤–Њ [3],
![]() ,
,
–≥–і–µ –Є–љ—В–µ–≥—А–∞–ї –њ–Њ–љ–Є–Љ–∞–µ—В—Б—П –≤ —Б–Љ—Л—Б–ї–µ –≥–ї–∞–≤–љ–Њ–≥–Њ –Ј–љ–∞—З–µ–љ–Є—П –њ–Њ –Ъ–Њ—И–Є, —Г—А–∞–≤–љ–µ–љ–Є–µ (16) —Б —Г—З–µ—В–Њ–Љ (5`), (17) вАУ (19), (22) вАУ (25) –Є –і–µ–ї–∞—П –љ–µ—Б–ї–Њ–ґ–љ—Л–µ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П, –њ—А–Є–≤–Њ–і–Є—В—Б—П –Ї —Б–Є–љ–≥—Г–ї—П—А–љ–Њ–Љ—Г –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–Љ—Г —Г—А–∞–≤–љ–µ–љ–Є—О [1, 3]:
–†–µ–Ї–Њ–Љ–µ–љ–і—Г–µ–Љ —Б–Ї–∞—З–∞—В—М –і—А—Г–≥–Є–µ —А–µ—Д–µ—А–∞—В—Л –њ–Њ —В–µ–Љ–µ: –њ–Њ–ї–Є—В–Њ–ї–Њ–≥–Є—П —И–њ–∞—А–≥–∞–ї–Ї–Є, —А–µ—Д–µ—А–∞—В –Љ–µ—В–∞–ї–ї—Л.
–Ъ–∞—В–µ–≥–Њ—А–Є–Є:
–Я—А–µ–і—Л–і—Г—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞ | 1 2 3 4 5 6 | –°–ї–µ–і—Г—О—Й–∞—П —Б—В—А–∞–љ–Є—Ж–∞ —А–µ—Д–µ—А–∞—В–∞
 –У–ї–∞–≤–љ–∞—П
–У–ї–∞–≤–љ–∞—П