Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Рассмотрение оператора дифференцирования как оператора, действующего из D1 в С[a,b], не вполне удобно, так как, хотя при этом мы и получаем непрерывный оператор, определенный на всем пространстве, но не к любой функции из D1 можно применять этот оператор дважды. Удобнее рассматривать оператор дифференцирования в еще более узком пространстве, чем D1 , а именно в пространстве  бесконечно дифференцируемых функций на отрезке [a; b], в котором топология задается счетной системой норм . Оператор дифференцирования переводит все это пространство в себя, и, как можно проверить, он непрерывен на этом пространстве.

2. Ограниченность и норма линейного оператора

Определение 2. Линейный оператор, действующий из Е в Е1, называется ограниченным, если он определен на всем Е и каждое ограниченное множество переводит снова в ограниченное. Между непрерывностью и ограниченностью линейного оператора существует тесная связь, т.е. справедливы следующие утверждения:

Теорема 1. Для того, чтобы линейный оператор  был непрерывным, необходимо и достаточно, чтобы он был ограничен.

1. Пусть оператор А неограничен. Тогда существует МЕ – ограниченное множество, такое, что множество АМЕ1 не ограничено. Следовательно, в Е1 найдется такая окрестность нуля V, что ни одно из множеств АМ не содержится в V. Но тогда существует такая последовательность хnM , что ни один из элементов Ахn не принадлежит V и получаем, что в Е, но  не сходится к 0 в Е; это противоречит непрерывности оператора А.

2. Если оператор А не непрерывен в точке 0, то в Е1 существует такая последовательность , что Ахn не стремится к 0. При этом последовательность  ограничена, а последовательность  не ограничена. Итак, если оператор А не непрерывен, то А и не ограничен. Утверждение доказано.

Если Е и Е1 – нормированные пространства, то условие ограниченности оператора А, действующего из Е в Е1, можно сформулировать так: оператор А называется ограниченным, если он переводит любой шар в ограниченное множество.

В силу линейности оператора А это условие можно сформулировать так: оператор А ограничен, если существует С=const , что для любого Е : .

Определение 3. Наименьшее из чисел С, удовлетворяющих этому неравенству, называется нормой оператора А и обозначается .

Теорема 2 [1]. Для любого ограниченного оператора А , действующего из нормированного пространства в нормированное .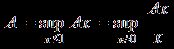

3. Сумма и произведение линейных операторов. Пространство линейных непрерывных операторов

Определение 4. Пусть А и В – два линейных оператора, действующих из линейного топологического пространства Е в пространство Е1. Назовем их суммой А+В оператор С, ставящий в соответствие элементу  элемент у=Ах+Вх, .

Можно проверить, что С=А+В – линейный оператор, непрерывный, если А и В непрерывны. Область определения DC оператора С есть пересечение  областей определения операторов А и В.

Если Е и Е1 – нормированные пространства, а операторы А и В ограничены, то С тоже ограничен, причем

 (2)

Действительно, для любых х , следовательно, выполняется неравенство (2).

Определение 5. Пусть А и В – линейные операторы, причем А действует из Е в Е1, а В действует из Е1 в Е2 . Произведением ВА операторов А и В называется оператор С, ставящий в соответствие элементу  элемент  из Е2.

Область определения DC оператора С=ВА состоит из тех хDA , для которых АхDB. Ясно , что оператор С линеен. Он непрерывен, если А и В непрерывны.

Если А и В – ограниченные операторы, действующие в нормированных пространствах, то и оператор С=ВА – ограничен, причем

 (3)

Действительно, , следовательно, выполняется (3).

Сумма и произведение трех и более операторов определяются последовательно. Обе эти операции ассоциативны.

Произведение оператора А на число к (обозначается кА) определяется как оператор, который элементу х ставит в соответствие элемент кАх.

Совокупность Z(E,E1) всех непрерывных линейных операторов, определенных на всем Е и отображающих Е в Е1 ( где Е и Е1– фиксированные линейные нормированные пространства), образует, по отношению к введенным операциям сложения и умножения на число, линейное пространство. При этом Z(E, E1) – нормированное пространстово (с тем определением нормы оператора, которое было дано выше).

4. Обратный оператор

Рекомендуем скачать другие рефераты по теме: бесплатные шпаргалки по праву, диплом.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата