Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Пусть А – линейный оператор, действующий из Е в Е1 , и DA область определения, а RA – область значений этого оператора.

Определение 6. Оператор А называется обратимым, если для любого уRA уравнение Ах=у имеет единственное решение.

Если А обратим, то любому элементу уRA можно поставить в соответствие единственный элемент хDA , являющийся решением уравнения Ах=у. Оператор, осуществляющий это соответствие, называется обратным к А и обозначается А-1.

Теорема 3 [1]. Оператор А-1, обратный линейному оператору А, также линеен.

Доказательство.

Достаточно проверить выполнение равенства

.

Положим Ах1=у1 и Ах2=у2, в силу линейности А имеем

 (*)

По определению обратного оператора А-1у1=х1 и А-1у2=х2, умножим оба равенства соответственно на  и :

.

С другой стороны из равенства (*) следует , следовательно, .

Теорема доказана.

Теорема 4 [3]. (Теорема Банаха об обратном операторе)

Пусть А – линейный ограниченный оператор, взаимно однозначно отображающий банахово пространство Е на банахово пространство Е1. Тогда обратный оператор А-1 ограничен.

Теорема 5 [3]. Пусть Е – банахово пространство, I – тождественный оператор в Е, а А – такой ограниченный линейный оператор, отображающий Е в себя, что . Тогда оператор (I-A)-1 существует, ограничен и представляется в виде .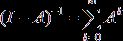

Доказательство.

Так как , то ряд 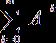 сходится. А так как  для всех , то ряд 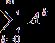 также сходится. Пространство Е полно, значит, из сходимости ряда  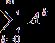вытекает, что сумма ряда 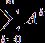представляет собой ограниченный линейный оператор. Для любого n имеем: 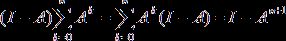, переходя к пределу и учитывая, что , получаем , следовательно .

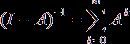Теорема доказана.

5. Спектр оператора. Резольвента.

Всюду, где речь идет о спектре оператора, считаем, что оператор действует в комплексном пространстве.

В теории операторов и ее применениях первостепенную роль играет понятие спектра оператора. Рассмотрим это понятие сначала применительно к операторам в конечномерном пространстве.

Пусть А – линейный оператор в n-мерном пространстве Еn . Число  называется собственным значением оператора А , если уравнение имеет ненулевые решения. Совокупность всех собственных значений называется спектром оператора А, а все остальные значения  – регулярными.

Иначе говоря,  есть регулярная точка, если оператор  обратим. При этом оператор -1 , как и любой оператор в конечномерном пространстве, ограничен, поэтому в конечномерном пространстве существует две возможности:

уравнение  имеет ненулевое решение, т. е.  есть собственное значение для А , оператор -1 при этом не существует;

Рекомендуем скачать другие рефераты по теме: бесплатные шпаргалки по праву, диплом.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата