
Оператор сдвига
| Категория реферата: Рефераты по математике
| Теги реферата: атлетика реферат, изложение 6 класс
| Добавил(а) на сайт: Гольдин.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата
существует ограниченный оператор ![]() -1, т.е.
-1, т.е. ![]() есть регулярная точка.
есть регулярная точка.
В бесконечномерном пространстве существует третья возможность:
оператор ![]() -1 существует, т.е. уравнение
-1 существует, т.е. уравнение ![]() имеет лишь нулевое решение, но этот оператор
не ограничен.
имеет лишь нулевое решение, но этот оператор
не ограничен.
Введем следующую терминологию. Число ![]() мы назовем регулярным для оператора А, действующего в (комплексном) линейном нормированном пространстве Е, если
оператор
мы назовем регулярным для оператора А, действующего в (комплексном) линейном нормированном пространстве Е, если
оператор ![]() -1 , называемый резольвентой оператора А , определен на всем Е и непрерывен.
Совокупность всех остальных значений
-1 , называемый резольвентой оператора А , определен на всем Е и непрерывен.
Совокупность всех остальных значений ![]() называется спектром оператора А . Спектру
принадлежат все собственные значения оператора А, так как если
называется спектром оператора А . Спектру
принадлежат все собственные значения оператора А, так как если ![]() х=0 при
некотором
х=0 при
некотором ![]() , то
, то ![]() -1 не
существует. Их совокупность называется точечным спектром. Остальная часть
спектра, т.е. совокупность тех
-1 не
существует. Их совокупность называется точечным спектром. Остальная часть
спектра, т.е. совокупность тех ![]() , для которых
, для которых ![]() -1 существует, но не непрерывен, называется непрерывным спектром. Итак, любое значение
-1 существует, но не непрерывен, называется непрерывным спектром. Итак, любое значение ![]() является для оператора А или регулярным, или
собственным значением, или точкой непрерывного спектра. Возможность наличия у
оператора непрерывного спектра – существенное отличие теории операторов в
бесконечномерном пространстве от конечномерного случая.
является для оператора А или регулярным, или
собственным значением, или точкой непрерывного спектра. Возможность наличия у
оператора непрерывного спектра – существенное отличие теории операторов в
бесконечномерном пространстве от конечномерного случая.
Теорема 6 [3]. Если А –ограниченный
линейный оператор в банаховом пространстве и ![]() , то
, то ![]() – регулярная
точка.
– регулярная
точка.
Доказательство.
Так как, очевидно ![]() , то
, то 
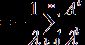 . При
. При ![]() этот ряд сходится (теорема 4), т.е. оператор
этот ряд сходится (теорема 4), т.е. оператор ![]() имеет ограниченный обратный. Иначе говоря, спектр оператора А содержится в круге радиуса
имеет ограниченный обратный. Иначе говоря, спектр оператора А содержится в круге радиуса ![]() с центром в нуле.
с центром в нуле.
Теорема доказана.
Пример. В пространстве ![]() функций, непрерывных на отрезке
функций, непрерывных на отрезке ![]() , рассмотрим
оператор А, определяемый формулой Аx(t)=M(t)x(t) , где M(t)– фиксированная
непрерывная функция. Возьмем произвольное число
, рассмотрим
оператор А, определяемый формулой Аx(t)=M(t)x(t) , где M(t)– фиксированная
непрерывная функция. Возьмем произвольное число ![]() , тогда
, тогда ![]() , а
, а ![]() .
.
Спектр рассматриваемого оператора
состоит из всех ![]() , для которых Если
функция M(t)-
, для которых Если
функция M(t)- ![]() обращается в
нуль при некотором t, заключенном между 0 и 1, то оператор
обращается в
нуль при некотором t, заключенном между 0 и 1, то оператор ![]() не определен на всем пространстве
не определен на всем пространстве ![]() , так как
функция
, так как
функция 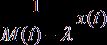 уже не обязана быть непрерывной. Если же
функция M(t)-
уже не обязана быть непрерывной. Если же
функция M(t)- ![]() не обращается в нуль на отрезке
не обращается в нуль на отрезке ![]() , то функция
, то функция 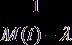 непрерывна на этом отрезке, а, следовательно, ограничена: для некоторого
непрерывна на этом отрезке, а, следовательно, ограничена: для некоторого ![]()
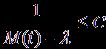 при всех
при всех ![]() .
Следовательно, оператор
.
Следовательно, оператор ![]() ограничен, а число
ограничен, а число ![]() – регулярное для оператора А. Таким образом, спектр оператора А есть совокупность всех значений функции M(t) на отрезке
[0;1], причем собственные значения отсутствуют, т.е. оператор умножения на t
представляет собой пример оператора с чисто непрерывным спектром.
– регулярное для оператора А. Таким образом, спектр оператора А есть совокупность всех значений функции M(t) на отрезке
[0;1], причем собственные значения отсутствуют, т.е. оператор умножения на t
представляет собой пример оператора с чисто непрерывным спектром.
Замечания
Любой ограниченный линейный оператор, определенный в комплексном банаховом пространстве, имеющем хоты бы один отличный от нуля элемент, имеет непустой спектр. Существуют операторы, у которых спектр состоит из единственной точки (оператор умножения на число).
Теорема 5 может быть уточнена
следующим образом. Пусть ![]() (можно доказать, что этот предел существует
для любого ограниченного оператора А), тогда спектр оператора А целиком лежит
внутри круга радиуса r с центром в нуле. Величина r называется спектральным
радиусом оператора А.
(можно доказать, что этот предел существует
для любого ограниченного оператора А), тогда спектр оператора А целиком лежит
внутри круга радиуса r с центром в нуле. Величина r называется спектральным
радиусом оператора А.
Резольвентные операторы ![]() и
и ![]() , отвечающие
точкам
, отвечающие
точкам ![]() и
и ![]() , перестановочны между собой и удовлетворяют соотношению
, перестановочны между собой и удовлетворяют соотношению ![]() , которое
легко проверить, умножив обе части этого равенства на
, которое
легко проверить, умножив обе части этого равенства на ![]() . Отсюда
вытекает, что если
. Отсюда
вытекает, что если ![]() – регулярная точка для А, то производная от
– регулярная точка для А, то производная от ![]() по
по ![]() при
при ![]() =
=![]() , т.е.
, т.е. 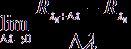 , существует
(в смысле сходимости по операторной норме) и равна
, существует
(в смысле сходимости по операторной норме) и равна ![]() .
.
§2. Унитарные операторы. Оператор сдвига
В этом разделе будем рассматривать пространство Н со скалярным произведением, которое является частным случаем нормированного пространства.
6. Оператор сдвига. Спектр оператора сдвига
Определение 7. Ограниченный линейный
оператор U в пространстве Н называется изометрическим, если он не изменяет
величины скалярного произведения: ![]() для любых
для любых ![]() .
.
В этом случае, если х=у, то ![]() , или
, или ![]() . Значит, изометрический оператор сохраняет норму элемента, а норма самого такого
оператора, как следует из определения нормы, равна 1 (
. Значит, изометрический оператор сохраняет норму элемента, а норма самого такого
оператора, как следует из определения нормы, равна 1 (![]() ).
).
Понятие изометрического оператора можно ввести также для операторов, действующих в нормированном пространстве.
Определение 8. Ограниченный линейный
оператор U в нормированном пространстве Е называется изометрическим, если он не
изменяет величины нормы: ![]() для любых
для любых ![]() .
.
Лемма 1. Для того, чтобы линейный
оператор U в пространстве Н был изометрическим, необходимо и достаточно, чтобы
выполнялось условие: ![]() для любых
для любых ![]() .
.
Доказательство. Нужно доказать только
достаточность. Для этого используем тождество ![]()
![]()
![]()
![]()
![]() . Его легко
проверить, если представить левую часть в виде скалярных произведений:
. Его легко
проверить, если представить левую часть в виде скалярных произведений: ![]()
![]()
![]()
![]()
![]() . Так как
левая часть не изменится при замене векторов
. Так как
левая часть не изменится при замене векторов ![]() на векторы
на векторы ![]() , то правая
тоже не изменится, т. е.
, то правая
тоже не изменится, т. е. ![]() .
.
Определение 9. Оператор U называется унитарным, если он изометрический и имеет обратный оператор, определенный на всем пространстве Н.
Теорема 7. Спектр унитарного оператора – это множество, лежащее на единичной окружности.
Рекомендуем скачать другие рефераты по теме: бесплатные шпаргалки по праву, диплом.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата
 Главная
Главная