Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Теорема 8. Пусть  и ; тогда оператор I – C непрерывно обратим. При этом справедливы оценки

 (1)

 (2)

Доказательство. Рассмотрим в L(X) ряд

I+C+C2+C3+… (3)

Так как , то ряд (3) оценивается сходящимся числовым рядом – геометрической прогрессией

По признаку Вейерштрасса ряд (3) сходится равномерно, т.е.

.

Где S – сумма ряда (3). Далее простой проверкой убеждаемся, что

,

.

Но при этом  (ибо  и ), а . Поэтому, в пределе имеем равенства (I – C)S = I и S(I – C) = I. По лемме 1 отсюда заключаем, что I – C непрерывно обратим и S=(I – C)-1. Далее,

,

.

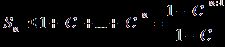Переходя в этих неравенствах к пределу при , получаем оценки (1) и (2). Теорема доказана.

Теперь рассмотрим более общий случай пространства L(X,Y). Пусть А Î L(X,Y) непрерывно обратим.

Теорема 9. Пусть A, B Î L(X,Y), А непрерывно обратим и выполнено неравенство . Тогда B непрерывно обратим и справедливы оценки

, .

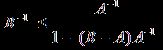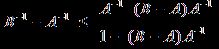§4. Абстрактные функции

Пусть S – некоторое множество на числовой оси или в комплексной плоскости, а X – нормированное пространство.

Рассмотрим функцию x() с областью определения S и с областью значений в X. Такие функции принято называть абстрактными функциями числовой переменной или векторными функциями числовой переменной, поскольку элементы линейного (иначе – векторного) пространства мы называем также векторами. На абстрактные функции числовой переменной переносятся многие понятия и факты математического анализа. Далее рассмотрим сведения о пределах и непрерывности таких функций, о разложении в степенные ряды, а также понятие аналитической абстрактной функции.

Пусть x() определена в окрестности точки 0, за исключением, быть может, самой точки 0. Элемент а Î X будем называть пределом функции x() при →0 и записывать

 при →0,

если  при →0.

Рекомендуем скачать другие рефераты по теме: реферат факторы, презентация дипломной работы.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата