Предыдущая страница реферата | 7  8  9  10  11  12  13  14  15  16  17 | Следующая страница реферата

Пусть  элементарная матрица порядка , тогда справедливо равенство:

1) ., т.е  получена из матрицы , умножением -строки на скаляр . Определитель матрицы .

Матрица  получена из  умножением -строки на скаляр , поэтому определитель

2)

Матрица, полученная из  прибавлением к -строке

Лемма 2

-элементарные матрицы

1) , доказательство следует из Леммы 1

2) , доказательство из утверждения (1) при условии

Теорема 1

Определитель произведения двух матриц равен произведению их определителей т.е.

Доказательство:

Пусть строки матрицы  линейно независимы, тогда существует цепочка элементарных преобразований 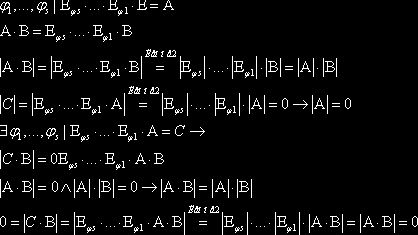, тогда по Лемме 2 следует, что . Из того, что () имеем: , тогда

2) Строки  линейно зависимы, тогда существует цепочка элементарных преобразований, которая переводит  в ступенчатую матрицу , у которой есть нулевая строка т.е. , . Тогда

Из того, что , в произведении , тоже есть нулевая строка, потому

Необходимые и достаточные условия равенства определителя нулю

 поле скаляров, ,-матрица над полем

Теорема 1

строки (столбцы) матрицы линейно зависимы

Достаточность:

Если строки (столбцы) матрицы линейно зависимы, то какая-то строка является линейной комбинацией других строк (по 8 свойсву определителей)

Необходимость:

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.





Предыдущая страница реферата | 7  8  9  10  11  12  13  14  15  16  17 | Следующая страница реферата