Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

II) Перестановка строк

Пусть  получена из перестановкой двух строк, тогда  получена из  перестановкой двух столбцов, тогда

III) Определитель матрицы, имеющий две одинаковые строки (столбца) равных нулю

Доказательство:

Проведем для такого поля , где

Замечание

Доказательство для случая найди в учебнике Куликовой Алгебра и теория чисел

Пусть в  есть две одинаковые строки с номерами и , где , поменяем местами строки и , получим матрицу

(по св.2)

 и , тогда

Если у  два одинаковых столбца, то у транспонированной матрицы  две одинаковые строки

IV) Если все элементы какой-либо строки (столбца) матрицы  умножить на , то определитель умножиться на

Доказательство:

Пусть  получена из  умножением на  строки

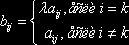
 так как , то

Аналогичное доказательство для столбцов

V) Определитель матрицы у которой две строки (столбца) пропорциональны равны нулю

Доказательство:

Пусть в матрице ,  строки  пропорциональны т.е -строка равна произведению  на -строку. Пусть

Для столбцов:

Пусть  получена из , . Столбцы  и  пропорциональны и

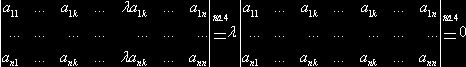
VI) Если каждый элемент -строки(столбца) квадратной матрицы  есть сумма двух элементов, то определитель  равен сумме двух определителей. В матрице первого определителя в - строке (столбце), записаны первые слагаемые, а в матрице второго определителя вторые слагаемые. Остальные элементы матриц этих определителей такие же как у матрицы

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.





Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата