Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата

Пусть . Докажем, что строки линейно зависимы. Предположим, что строки  линейно независимы, тогда существует цепочка элементарных преобразований переводящее . Из доказанного в пункте II следует, что . Получили противоречье . Докажем, что если -строка матрицы  линейно зависима,, но (числа векторов столбца)  линейно зависима.

Теорема 2

 следующие условия равносильны:

1)

2) -линейно зависимы

3) -обратима

4)  представима в виде произведения элементарных матриц

Доказательство:

 доказано в Теореме 1

§6 Разбиение матриц

Если  матрицу ,  матрицу ,  матрицу  и  матрицу  записать в виде

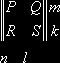
 (1)

То они, образуют некоторую  матрицу . В таком случае  могут быть названы блоками матрицы . И обозначены  соответственно. Представление (1) называется разбиением матрицы .

Если матричное произведение существует и , разбиты на блоки , , а разбиение по столбцам матрицы  соответствует разбиению по строкам матрицы , то можно ожидать, что  имеет блоки , задаваемые формулой

Таким образом, мы предполагаем, что произведение матриц в терминах блоков, полученных при соответствующих разбиениях сомножителей, формально совпадает с произведением этих матриц в терминах скалярных элементов. Покажем это на примере:

Упражнение1. Пусть

, ,

, ,

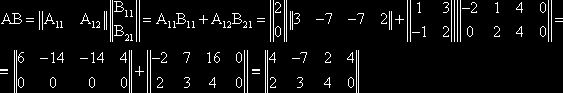
Это проверяется прямым вычислением

Теорема (1)

Пусть матрица  из  имеет блоки , где матрица, , и  матрица из  с блоками размера . Тогда  имеет блоки

Доказательство. Отметим, что каждое произведение существует и является  матрицей. Следовательно,  существует и будет  матрицей. Для фиксированного каждое  имеет  столбцов и для фиксированного  каждое  имеет строк, откуда следует, что блоки некоторой  матрицы .

Пусть некоторый элемент матрицы , расположенный в клетке  блока . Так как , есть сумма элементов в клетках и матриц , . Но элемент матрицы в клетке  является суммой произведений элементов в строке матрицы  на элементы столбца матрицы . Далее, элементы строки матрицы  совпадают с некоторыми элементами  строки в , а именно, с , где индекс  определяется неравенствами

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.





Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата