Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Матрица, составленная из элементов, находящихся на пересечении нескольких выбранных строк матрицы  и нескольких выбранных столбцов, называется субматрицей для матрицы . Если -номера выбранных строк и -номера выбранных столбцов, то субматрица это

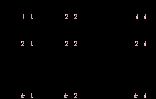
В частности, строки и столбцы матрицы можно рассматривать как ее субматрицы.

§2 Операции над матрицами

Определим следующие операции:

Сумма двух  матриц , и  с элементами  и есть  матрица С с элементами , запишем это как

Произведение матрицы  на число поля есть матрица С с элементами , запишем как .

Произведение  матрицы на матрицу есть матрица С с элементами , запишем

 поле скаляров, рассмотрим 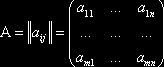, где элемент матрицы , расположенный в -строке , -столбце . Размерность матрицы .Если , то -квадратная матрица порядка . Множество -это множество всех  матриц над полем .

Опр. Две матрицы равны, если они имеют одинаковую размерность и на одинаковых местах расположены одинаковые элементы. Другими словами:  равна матрице , т.е

Опр. Пусть -это матрицы одинаковой размерности . Суммой матриц  и  называется матрица у которой в строке,  столбце расположен элемент , т.е. . Другими словами: Чтобы сложить две матрицы нужно сложить соответствующие элементы:

Пример:

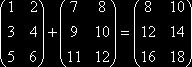
Опр. Пусть , , . Произведение скаляра  на матрицу  называется  у которой в строке,  столбце расположен элемент . Другими словами: Чтобы скаляр  умножить на матрицу  нужно все элементы матрицы  умножить на скаляр .

Определение. Противоположной к матрице  называется матрица

Свойства сложения и умножения матриц на скаляры:

-абелева группа

1) Сложение матриц  ассоциативно и коммутативно.

2)

3)

а)

б)

4)

Глава II

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата