Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата



Наличие квадратного уравнения и условие единственности решения, естественно приведут к поиску корней дискриминанта. Вместе с тем условие x ¹ - 3 должно привлечь внимание. И “тонкий момент” заключается в том, что квадратное уравнение системы может иметь два корня! Но обязательно только один из них должен равняться - 3. Имеем D = a2 - 4, отсюда D = 0, если a = ± 2; x = - 3 — корень уравнения x2 - ax + 1 = 0 при a = - 10 / 3, причём при таком значении a второй корень квадратного уравнения отличен от - 3.

Ответ: a = ± 2 или a = - 10 / 3.

Пример 10.51. При каких a уравнение ax2 = a2 равносильно неравенству

| x - 3| ³ a?

Решение. При a ¹ 0 уравнение имеет единственное решение, а неравенство — бесконечно много. Если a = 0, то решением как уравнения, так и неравенства является всё множество действительных чисел. Следовательно, требованию задачи удовлетворяет только a = 0.

Ответ: a = 0.

Пример 10.52. Решить уравнение с параметрами

(a2 - 9)x = a2 + 2a - 3.

Решение. Уравнение имеет смысл при любых значениях параметра. Запишем уравнение в виде:

(a - 3)(a + 3)x = (a + 3)(a - 1).

Если a = - 3, то уравнение принимает вид: 0x = 0. Отсюда следует, что при x Î R, т.е. решением уравнения является любое действительное число. Если a ¹ - 3, то уравнение принимает вид: (a - 3)x = a - 1.При a = 3 имеем 0x = 2. Уравнение решения не имеет. При a ¹ - 3 имеем x = (a - 1) / (a - 3). Уравнение имеет единственное решение (например, x = 3 при a = 4, x = 3 / 5 при a= - 2 и т.д.)

Ответ: a = - 3, x Î R; a = 3, x Î Æ ; a ¹ ± 3, x = (a - 1) / (a - 3).

Пример 10.53.

(x - 4) / (x + 1) - 1 / a(x + 1) = - 2 / a.

Решение. Очевидно, (x + 1)a ¹ 0, т.е. x ¹ - 1, a ¹ 0. Преобразуем данное уравнение, умножив обе его части на a(x + 1) ¹ 0:

(x - 4)a - 1 = - 2(x + 1), т.е. (a + 2)x = 4a - 1.

Если a = - 2, то имеем 0х = - 9. Следовательно, xÎ Æ . Если a ¹ - 2, то x = (4a +1) / (a + 2). Но, как мы уже отметили, x ¹ - 1. Поэтому надо проверить, нет ли таких значений a при которых найденное значение x равно - 1.

(4a - 1) / (a + 2) = - 1, т.е. 4a - 1 = - a - 2, т.е. 5a = - 1, a= - 1 / 5.

Значит, при a ¹ 0, a ¹ - 2, a ¹ - 1 / 5 уравнение имеет единственное решение (4a - 1) / (a + 2).

Ответ: x Î Æ при a Î {- 2, 0, - 1 / 5}; x = (4a - 1) / (a + 2) при aÏ {- 2, 0, - 1 / 5}.

Пример 10.54.

(a - 5)x2 + 3ax - (a - 5) = 0.

Решение. При (a - 5) = 0, т.е. a = 5 имеем 15x - 0 = 0, т.е. x = 0. При a - 5 ¹ 0, т.е. a ¹ 5 уравнение имеет корни

X1,2 = (- 3a ± Ö (9a2 + 4(a - 5)2)) / (2(a - 5)).

Ответ: x = 0 при a = 5; x = (- 3a ± Ö (9a2 + 4(a - 5)2)) / (2(a - 5)) при a ¹ 5.

Пример 10.55.

1 / (x - 1) + 1 / (x - a) = (a + 1) / a.

Решение. Отмечаем, что a(x - 1)(x - a) ¹ 0, т.е. x ¹ 1, x ¹ a, a ¹ 0. При этих условиях данное уравнение после упрощений принимает вид

(a + 1)x2 - (a2 + 4a + 1)x + (2a2 + 2a) = 0.

Если a +1 = 0, т.е. a = - 1, имеем, 2x = 0, т.е. x = 0.

Если a + 1 ¹ 0, т.е. a ¹ - 1, то находим, что

x1,2 = (a2 + 4a + 1 ± Ö (a4 + 2a2 + 1)) / (2(a +1) = (a2 + 4a + 1 ± (a2 + 1) ) / (2(a + 1))

т.е. x1 = a + 1, x2 = 2a / (a + 1). Найдём значения a, при которых x = 1 и x = a, чтобы исключить их.

a + 1 = 1 Þ a = 0 — недопустимо по условию;

a + 1 = a Þ 1 = 0 — невозможно;

2 / (a + 1) = 1 Þ 2a = a + 1, т.е. a = 1;

2 / (a + 1) = a Þ 2a = a2 + a, a = 1 и a = 0 — недопустимо.

Итак, если a ¹ - 1, a ¹ 0, a ¹ 1, то x1 = a + 1, x2 = 2a / (a + 1).

Теперь рассмотрим, что происходит с уравнением при a = 1. Найдём корни уравнения: x1 = 1 и x2 = 2, причём x1 = 1 не подходит по условию. Теперь выписываем

Ответ: x1 = a + 1 и x2 = 2 при a ¹ 0, a ¹ ± 1; x = 0 при a = - 1; x = 2 при a = 1.

Пример 10.56. При каких значениях a система уравнений

Имеет единственное решение?

Решение. Умножим второе уравнение на a и вычтем его из первого уравнения. Получаем равносильную систему

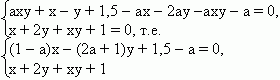
Если a = 1, то - 3y + 0,5 = 0, т.е. y = 1 /6. Подставив это значение во второе уравнение, находим единственное значение x. Система имеет единственное решение.

Если a = - 0,5, то система имеет единственное решение. При остальных значениях a сведём систему к квадратному уравнению; из первого уравнения системы находим

y = ((1 - a)x + 1,5 - a) / (2a + 1),

подставляем во второе уравнение:

x + ((2 - 2a)x + 3 - 2a) / (2a + 1) + ((1 - a)x2 + 1,5x - ax) / (2a + 1) +1 = 0, т.е.

2ax + 3x - 2ax + 3 - 2a + x2 - ax2 +1,5x - ax + 2a + 1 = 0,

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, научный журнал.

Предыдущая страница реферата | 16  17  18  19  20  21  22  23  24  25  26 | Следующая страница реферата