Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

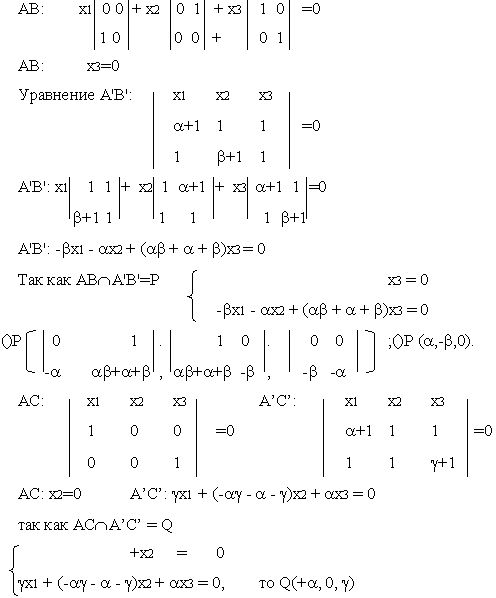
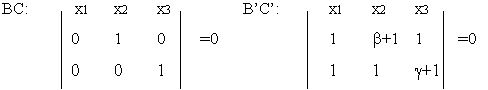
так как R= BCÇ B’C’

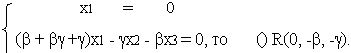
С помощью условия коллинеарности трех () убедимся, что () P,Q,R лежат на одной прямой.

Имеем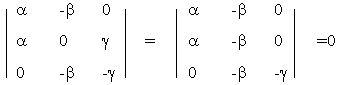

Условие коллинеарности выполнено, следовательно, P,Q,R Î одной прямой.

Теорема доказана.

Глава 3. Аксиоматическое построение проективной плоскости. 3.1. Аксиоматика аффинной плоскости.

Начнем с некоторых наиболее простых фактов обычной плоской геометрии, которые мы применим в качестве аксиом при синтетическом построении теории.

Определение: Аффинной плоскостью называют множество элементов, именуемых точками и систему его подмножеств, именуемых прямыми, причем должны выполнятся три формулируемые ниже аксиомы А1-А3.

А1: Для " двух различных точек Р и Q $ единственная прямая, проходящая через них.

Две прямые называются параллельными, если они совпадают или не имеют общих точек.

А2: Для " заданной прямой l и точки Р $ одна и только одна проходящая через Р прямая m: m || l

А3: $ три неколлинеарные точки (Точки Р1,Р2,…Рn называются коллинеарными, если $ прямая l, что все эти точки ей принадлежат).

Пример: Евклидова плоскость Е2 удовлетворяет аксиомам А1-А3, то есть является аффинной плоскостью.

Пример: Аффинная плоскость имеет, по крайней мере, четыре различных точки; плоскость состоящая ровно из четырех () существует.

Действительно в силу А3 на плоскости есть три неколлинеарные точки; обозначим их через P,Q,R. Согласно А2, $ прямая l , проходящая через Р и параллельной прямой QR, соединяющей Q и R (эта прямая $ по А1). Точно так же доказывается $ прямой

m || PQ, проходящей через R.

Покажем теперь, что l || m.

же S¹ R. Таким образом, четвертая () S необходимо должна существовать и наше первое утверждение доказано.

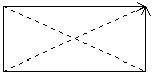
Теперь рассмотрим прямые PR и QS. Они могут пересекаться, но они могут и не пересекаться - это не противоречит аксиомам.

В этом случае мы получаем аффинную плоскость, содержащую ровно четыре () P,Q,R,S и шесть прямых PQ,РR,PS,QR,QS,RS.

Аксиомы А1-А3 здесь выполняются, таким образом, мы получим аффинную плоскость , содержащую наименьшее возможное число (), а именно, четыре.

3.2. Аксиоматика проективной плоскости.

Определение: Проективной плоскостью S называют множество, элементами которого именуются точками, и набор его подмножеств, именуемых прямыми, если при этом выполняются следующие четыре аксиомы.

П1.Через две различные точки P и Q плоскости S можно провести единственную прямую.

Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.





Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата