Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Доказательство: Пусть . Так как b¹ 0, то e >0. Пусть N – номер, соответствующий этому e , начиная с которого выполняется неравенство:

|yn-b|<e или |yn-b|<

из этого неравенства следует, что при n³ N выполняется неравенство |yn|>. Поэтому при n³ N имеем . Следовательно, начиная с этого номера N, мы можем рассматривать последовательность , и эта последовательность ограничена. Лемма доказана.

ТЕОРЕМА: Частное двух сходящихся последовательностей {xn} и {yn} при условии, что предел {yn} отличен от ноля, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}.

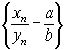Доказательство: Из доказанной ранее леммы следует, что, начиная с некоторого номера N, элементы последовательности {yn} отличны от ноля и последовательность ограничена. Начиная с этого номера, мы и будем рассматривать последовательность . Пусть а и b – пределы последовательностей {xn} и {yn}. Докажем, что последовательность бесконечно малая. В самом деле, так как xn=а+a n, yn=b+b n, то

.

Так как последовательность ограничена, а последовательность бесконечно мала, то последовательность 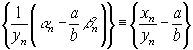бесконечно малая. Теорема доказана.

Итак, теперь можно сказать, что арифметические операции над сходящимися последовательностями приводят к таким же арифметическим операциям над их пределами.

ТЕОРЕМА: Если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравентству xn³ b (xn£ b), то и предел а этой последовательности удовлетворяет неравенству а³ b (a£ b).

Доказательство: Пусть все элементы xn, по крайней мере начиная с некоторого номера, удовлетворяют неравенству xn³ b. Предположим, что а<b. Поскольку а – предел последовательности {xn}, то для положительного e =b-a можно указать номер N такой, что при n³ N выполняется неравенство

|xn-a|<b-a.

Это неравенство эквивалентно

-(b-a)<xn-a<b-a

Используя правое из этих неравенств мы получим xn<b, а это противоречит условию теоремы. Случай xn£ b рассматривается аналогично. Теорема доказана.

Рекомендуем скачать другие рефераты по теме: рефераты по истории, доклад на тему биология.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата