Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



запишем целое число n по двоичной системе:

n=2m+e 12m-1+e 22m-2+…+e m (e 1, e 2, …, e m = 0 или 1)

согласно предположению

.

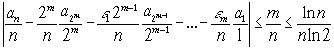Применяя теорему (1) для данных:

s0=0, s1=, sm-1=, sm=, …, pn0=0, pn1=, …, pn, m-1=,

, pn, m+1=0, …,

заключаем, что . Наконец, в силу (*) имеем:

.

 

ЗАДАЧА № 3

Если общий член ряда, не являющегося ни сходящимся, ни расходящимся в собственном смысле, стремится к нулю, то частичные суммы этого ряда расположены всюду плотно между их нижним и верхним пределами lim inf и lim sup.

РЕШЕНИЕ:

Нам достаточно рассмотреть случай, когда частичные суммы s1, s2, …, sn, … ограничены. Пусть , , l - целое положительное число, l>2 и .

Разобьем числовую прямую на l интервалов точками

-¥ , m+d , m+2d , …, M-2d , M-d , +¥ .

Выберем такое N, чтобы для n>N выполнялось неравенство |sn-sn+1|<d . Пусть, далее, sn1 (n1>N) лежит в первом интервале и sn2 (n2> n1) – в последнем. Тогда числа конечной последовательности не смогут “перепрыгнуть” ни один из l-2 промежуточных интервалов длиной d . Аналогично рассуждаем и в том случае, когда последовательность будет не “медленно восходящей”, а “медленно нисхожящей”.

Рекомендуем скачать другие рефераты по теме: рефераты по истории, доклад на тему биология.

Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата