Теория цепных дробей Содержание

Введение

Глава I. ПРАВИЛЬНЫЕ КОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ

§1. Представление рациональных чисел цепными дробями

§2. Подходящие дроби. Их свойства

Глава II. БЕСКОНЕЧНЫЕ ЦЕПНЫЕ ДРОБИ

§1. Представление действительных иррациональных чисел правильными бесконечными цепными дробями

1.1. Разложение действительного иррационального числа в правильную бесконечную цепную дробь

1.2. Сходимость правильных бесконечных цепных дробей

1.3. Единственность представления действительного иррационального числа правильной бесконечной цепной дробью

§2. Приближение действительного числа рациональными дробями с заданным ограничением для знаменателя

2.1. Оценка погрешности при замене действительного числа его подходящей дробью

2.2. Приближение действительного числа подходящими дробями

2.3. Теорема Дирихле

2.4. Подходящие дроби как наилучшие приближения

§3. Квадратические иррациональности и периодические цепные дроби

§4. Представление действительных чисел цепными дробями общего вида

Решение задач

Заключение

Используемая литература

Введение

Целью моей курсовой работы является исследование теории цепных дробей. В ней я попытаюсь раскрыть свойства подходящих дробей, особенности разложения действительных чисел в неправильные дроби, погрешности, которые возникают в результате этого разложения, и применение теории цепных дробей для решения ряда алгебраических задач.

Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение.

Работы Эйлера по теории цепных дробей были продолжены М. Софроновым (1729-1760), академиком В.М. Висковатым (1779-1819), Д. Бернулли (1700-1782) и др. Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений.

Глава I. Правильные конечные цепные дроби. §1. Представление рациональных чисел цепными дробями.

Целое число, являющееся делителем каждого из целых чисел 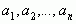, называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел.

Пусть 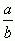- рациональное число, причем b>0. Применяя к a и b алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств:

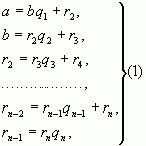
Рекомендуем скачать другие рефераты по теме: курсовая работа по учету, дипломная работа по праву.





1  2  3  4  5  6  7  8 | Следующая страница реферата