Claw.ru | Рефераты по математике | Теория цепных дробей Теория цепных дробей | Категория реферата: Рефераты по математике | Теги реферата: республика реферат, дипломная работа по праву | Добавил(а) на сайт: Ven'jamin. Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата 2

3

11

14

25

114

367

Подходящие дроби () равны соответственно ; ; ; ; ; ; ; .

Практически нахождение неполных частных и подходящих дробей удобно объединить в одну краткую схему, которую приведем для =(2, 3, 1, 4, 2)

.

А сейчас рассмотрим ряд свойств подходящих дробей.

Теорема: При k=1, 2, …, n выполняется равенство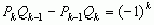

Доказательство: Проведем индукцию по k:

При k=1 равенство справедливо, так как .

Пусть это равенство верно при некотором k=n ().

Докажем справедливость равенства при k=n+1.

, то есть равенство верно при k=n+1.

Согласно принципу полной математической индукции равенство верно для всех k().

Теорема: Числитель и знаменатель любой подходящей дроби – взаимно простые числа, то есть всякая k–подходящая дробь несократима.

Доказательство: Докажем это свойство методом от противного. По предыдущему свойству имеем .

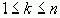
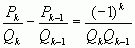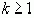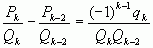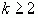Пусть , то есть , тогда из равенства следует, что делится на без остатка, что невозможно. Значит, наше допущение неверно, а верно то, что требовалось доказать, то есть .

Теорема: При () ()

Доказательство: Первое соотношение можно получить из равенства , доказанного выше, путем деления обеих частей на . Получаем

, что и требовалось доказать.

Докажем второе соотношение.

.

Теорема доказана полностью.

Теорема: Знаменатели подходящих дробей к цепной дроби, начиная с первого, образуют монотонно возрастающую последовательность, то есть 1=.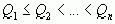

Доказательство: , , так что и положительны.

Рекомендуем скачать другие рефераты по теме: курсовая работа по учету, дипломная работа по праву.





Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата