
Теория цепных дробей
| Категория реферата: Рефераты по математике
| Теги реферата: республика реферат, дипломная работа по праву
| Добавил(а) на сайт: Ven'jamin.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8
Доказательство: Из формулы (5) следует
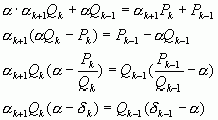
Но 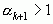 ,
, 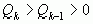 , так что
, так что 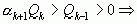
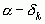 ) и (
) и (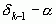 ) имеют одинаковый
знак, а это значит, что
) имеют одинаковый
знак, а это значит, что 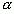 находится между
находится между 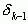 и
и 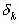 ;
;
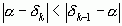 , то есть
, то есть 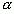 ближе к
ближе к 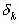 ,
чем к
,
чем к 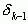 .
.
Теорема доказана.
Так как 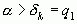 , то
, то 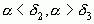 , и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей:
, и так далее; отсюда приходим к следующему заключению о взаимном расположении подходящих дробей:
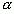 больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;
подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка – убывающую (в случае иррационального
больше всех подходящих дробей нечетного порядка и меньше всех подходящих дробей четного порядка;
подходящие дроби нечетного порядка образуют возрастающую последовательность, а четного порядка – убывающую (в случае иррационального 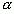
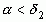
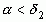 указанные последовательности являются бесконечными), то есть
указанные последовательности являются бесконечными), то есть
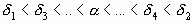
(в случае рационального 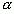
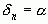 ).
).
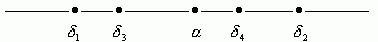
Учитывая то, что при 
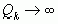 , вследствие чего
, вследствие чего 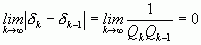 , переходим к дальнейшему выводу, что в случае иррационального
, переходим к дальнейшему выводу, что в случае иррационального 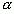 сегменты
сегменты 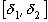 ,
, 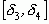 , … образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей
, … образуют стягивающуюся последовательность, которая, как известно, должна иметь единственную общую точку, являющуюся общим пределом последовательностей 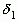 ,
, 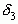 , … и
, … и 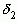 ,
, 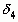 , … . Но так как
, … . Но так как 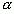 принадлежит всем сегментам последовательности, то
принадлежит всем сегментам последовательности, то 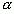 и совпадает с указанной точкой, так что
и совпадает с указанной точкой, так что 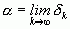 .
.
Итак, мы имеем следующий важный результат:
бесконечная последовательность подходящих дробей 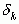 , которая возникает при разложении иррационального
, которая возникает при разложении иррационального 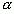 , сходится к
, сходится к 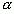 , колеблясь около него. Или: иррациональное действительное
, колеблясь около него. Или: иррациональное действительное 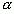 равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части).
равно пределу последовательности подходящих дробей своего разложения в бесконечную непрерывную дробь (процессом выделения целой части).
Теперь покажем, что сходящейся является последовательность подходящих дробей не только такой бесконечной непрерывной дроби, которая возникает при разложении иррационального числа 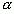 , но и любой бесконечной непрерывной дроби
, но и любой бесконечной непрерывной дроби 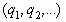 , где
, где 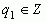 , а
, а 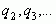 - произвольно выбранные целые положительные числа.
- произвольно выбранные целые положительные числа.
Но для этого мы заново исследуем взаимное расположение подходящих дробей.
С этой целью рассмотрим формулы:
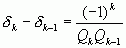 (1) и
(1) и 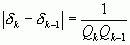 (2),
(2),
которые справедливы для любой бесконечной непрерывной дроби.
Формула (1) показывает, что любая подходящая дробь четного порядка больше двух соседних подходящих дробей, у которых порядок на единицу меньше или больше, чем у нее, то есть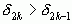 и
и 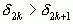 . Согласно
этому
. Согласно
этому 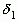 и
и 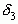 расположены слева
от
расположены слева
от 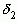 ,
, 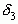 и
и 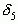 – слева от
– слева от 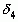 и так далее.
Формула (2) показывает, что расстояние между соседними подходящими дробями
при увеличении k убывает. Действительно, так как
и так далее.
Формула (2) показывает, что расстояние между соседними подходящими дробями
при увеличении k убывает. Действительно, так как 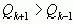 ,
то
,
то
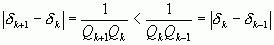
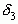 ближе к
ближе к 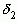 ,
чем
,
чем 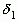 , а так как
, а так как 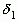 и
и 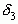 находятся слева от
находятся слева от 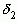 , то
, то 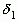
Скачали данный реферат: Милия, Майя, Kolodezev, Kas'jan, Syrovoj, Сердюков.
Последние просмотренные рефераты на тему: отчет по практике, реферат методы, шпоры по физике, защита диплома.
Категории:
Предыдущая страница реферата | 1 2 3 4 5 6 7 8
 Главная
Главная