Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата

1. Строим параллелограмм ОАСВ: АМ II ОВ, ВН II ОА.

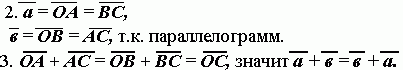
Для доказательства ассоциативности мы отложим от произвольной точки О вектор , от точки А вектор и от точки в – вектор с. Тогда мы имеем:

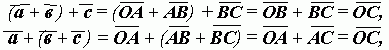
откуда и следует равенство Заметим, что приведенное доказательство совсем не использует чертежа. Это характерно ( при некотором навыке ) для решения задач при помощи векторов.

Остановимся теперь на случае, когда векторы и направлены в противоположные стороны и имеют равные длины; такие векторы называют противоположными. Наше правило сложения векторов приводит к тому, что сумма двух противоположных векторов представляет собой “вектор”, имеющий нулевую длину и не имеющий никакого направления; этот “вектор” изображается “отрезком нулевой длины”, т.е. точкой. Но это тоже вектор, который называется нулевым и обозначается символом 0. Равенство векторов.

Два вектора называются равными, если они совмещаются параллельным переносом. Это означает, что существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого вектора.

Из данного определения равенства векторов следует, что разные векторы одинаково направлены и равны по абсолютной величине.

И обратно: если векторы одинаково направлены и равны по абсолютной величине, то они равны.

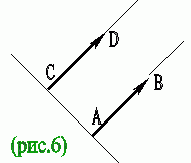
Действительно, пусть векторы и – одинаково направленные векторы, равные по абсолютной величине (рис.6). Параллельный перенос, переводящий точку С в точку А, совмещает полупрямую СD с полупрямой АВ, так как они одинаково направлены. А так как отрезки АВ и CD равны, то при этом точка D совмещается с точкой В, то есть параллельный перенос переводит вектор в вектор . Значит, векторы и равны, что и требовалось доказать.

Скалярное произведение двух векторов и его свойства.

Скалярным произведением двух нулевых векторов называется число, равное произведению числовых значений длин этих векторов на косинус угла между векторами.

Обозначение:.

Свойства скалярного произведения:

1. х = х.

2. Для того, чтобы два нулевых вектора а и в были перпендикулярны, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. х = 0.

3. Выражение х будем обозначать 2 и называть скалярным квадратом вектора . Свойства операций над векторами.

Имеют место следующие теоремы об операциях над векторами, заданными в координатной форме.

1. Пусть даны = (ах, аy, аz) и = ( вx, ву, вz), тогда сумма этих векторов есть вектор , координаты которого равны сумме одноименных координат слагаемых векторов, т.е. = + = (ах + вx; аy + ву; аz + вz).

Пример 1. = ( 3; 4; 6) и = ( -1; 4; -3), тогда = ( 3 + ( -1); 4 + 4; 6 + (-3)) = ( 2; 8; 3).

2. = (ах, аy, аz) и = ( вx, ву, вz), тогда разность этих векторов есть вектор , координаты которого равны разности одноименных координат данных векторов, т.е. = - = (ах - вx; аy - ву; аz - вz).

Пример 2.

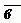= ( -2; 8; -3) и = ( -4; -5; 0), тогда с = – = ( -2 – ( -4 ); 8 – ( -5 ); -3 –0 ) = ( 2; -13; -3).

3. При умножении вектора = (ах, аy, аz) на число м все его координаты умножаются на это число, т.е. м = ( мах, маy, маz).

Пример 3.

= ( -8; 4; 0) и м = 3, тогда 3 = ( -8 х 3; 4 х 3; 0 х 3) = ( -24; 12; 0).

Понятие вектора, которое нашло широкое распространение в прикладных науках, явилось плодотворным и в геометрии. Аппарат векторной алгебры позволил упростить изложение некоторых сложных геометрических понятий, доказательства некоторых теорем школьного курса геометрии, позволил создать особый метод решения различных геометрических задач.

Рекомендуем скачать другие рефераты по теме: оформление доклада, онегин сочинение.





Предыдущая страница реферата | 1  2  3  4  5 | Следующая страница реферата